
こんにちは、ヒガシです。
今回も前回に引き続きshapを使って遊んでみようと思います。
前回の記事では、簡単な4入力、1出力のモデルにshapを適用し、各入力が出力に与える寄与度を分析してみました。
今回は前回のモデルを入力はそのままに出力を2つに増やしたモデルに改造し、そのモデルに対して再びshapを適用し、各出力ごとに入力の寄与度を見てみようと思います。
それではさっそくやっていきましょう!
使用するサンプルデータの紹介
前回に引き続き、以下のような簡単な数式を使って構築したデータを使用していきます。
※shapで出てきた結果が直観的にあっているのかわかりやすくするため。
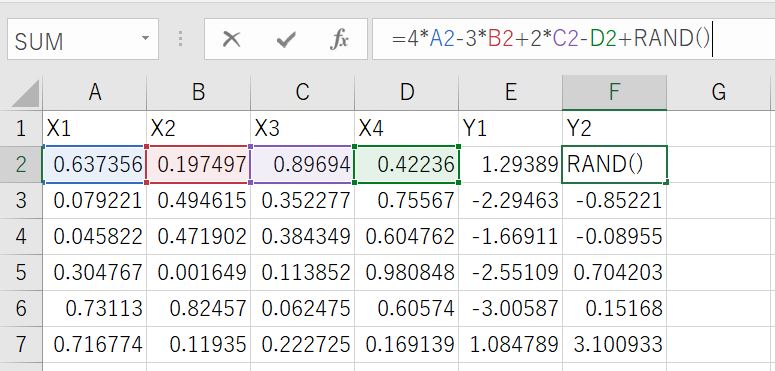
このデータは
Y1=X1-2*X2+3*X3-4*X4+乱数
Y2=4*X1-3*X2+2*X3-X4+乱数
という数式で構成されています。
つまり、Y1に対してはX1~X4に向かうにしたがって寄与度が大きくなり、逆にY2に対しては、X1~X4に向かうにしたがって寄与度が小さくなっていきます。
shapで出来てた結果が本当にこのようになっているのか確認していってきましょう。
KerasでAIモデルの構築
先ほど構築したデータを使って実際にAIモデルを構築してみましょう。
今回もKerasのSequentialモデルを使って構築していきます。
以下がそのコードです。
先ほどのデータがsample_data_shap2.csvという名前でプログラム実行フォルダに入っていることを前提に書いています。
#ライブラリ読み込み
from keras.models import Sequential
from keras.layers import Flatten, Dense
from tensorflow.keras.optimizers import Adam
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
#データ読み込み
data=pd.read_csv('sample_data_shap2.csv').values
Xdata=data[:,:-2]
Ydata=data[:,-2:]
#モデル構築
model=Sequential()
model.add(Dense(100,input_shape=(4,)))
model.add(Dense(100))
model.add(Dense(2))
model.compile(loss='mean_squared_error', optimizer=Adam(lr=0.0001), metrics=['mae'])
model.summary()
history =model.fit(Xdata, Ydata, validation_split=0.2, epochs=200, batch_size=16)
# 損失のplot
plt.plot(history.history['loss'], marker='.', label='loss')
plt.plot(history.history['val_loss'], marker='.', label='val_loss')
plt.title('model loss')
plt.grid()
plt.ylim(0,2)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(loc='best')
plt.show()
こいつを実行すると以下のグラフが出力されました。
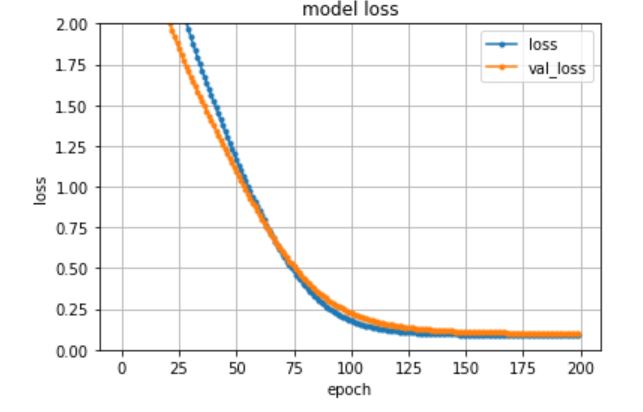
問題なく学習できていそうですね。
複数出力を持つモデルにshapを適用した結果
それでは先ほどのモデルにshapを適用してみましょう。
以下がそのコードです。
import shap
shap.initjs()
Xname=['X1','X2','X3','X4']
explainer = shap.KernelExplainer(model.predict, Xdata)
shap_values=explainer.shap_values(Xdata)
shap.summary_plot(shap_values, Xdata, feature_names=Xname, plot_type='bar', class_names=['Y1','Y2'])
こいつを実行すると以下の結果が得られました。
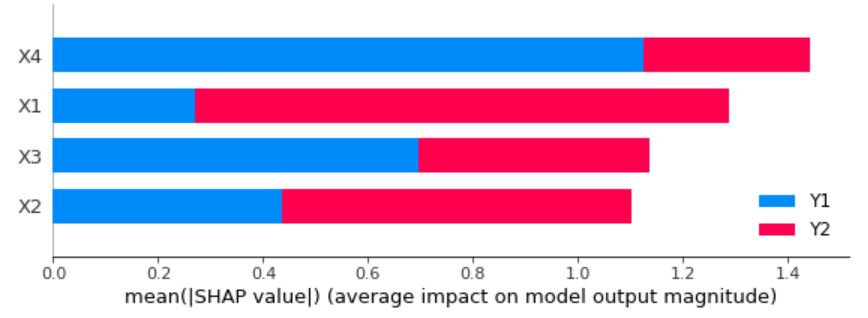
Y1(青い棒グラフ)に着目すると、X1~4に向かうにしたがって寄与度が大きくなっていることがわかると思います。
一方でY1(赤い棒グラフ)に着目すると、X1~4に向かうにしたがって寄与度が小さくなっていることがわかると思います。
というわけで問題なく寄与度の分析はできていそうですね。
(縦の並びがごちゃ混ぜなので少しわかりにくいですね。)
出力ごとに分けて寄与度を分析したい場合
先ほどの結果は棒グラフの縦の並びがごちゃごちゃしていてちょっとわかりにくかったですよね。
というわけで次は出力ごとに寄与度を分けて出力してみようと思います。
shapの機能を使ってもすぐにできますが、グラフの描写をアレンジしたりできませんので、今回はmatplotlibで自分でグラフを書いていってきましょう。
以下がそのコードです。
#shap_valuesから各出力に対する平均寄与度を算出する
shap_data=[]
for j in range(2):#2出力モデル
shap_y=[]
for i in range(4):#4入力モデル
shap_y.append(np.average(abs(np.array(shap_values)[j][:,i])))
shap_data.append(shap_y)
shap_data=np.array(shap_data)
#算出した平均寄与度からY1の結果を表示する
plt.bar(Xname,shap_data[0],label='Y1')
plt.legend(loc='upper left',fontsize=14)
plt.ylabel('shap_value',fontsize=14)
plt.ylim(0,1.2)
plt.show()
#算出した平均寄与度からY2の結果を表示する
plt.bar(Xname,shap_data[1],label='Y2')
plt.legend(loc='upper right',fontsize=14)
plt.ylabel('shap_value',fontsize=14)
plt.ylim(0,1.2)
plt.show()
こいつを実行すると以下の結果がえられました。
★Y1に対する寄与度分析の結果
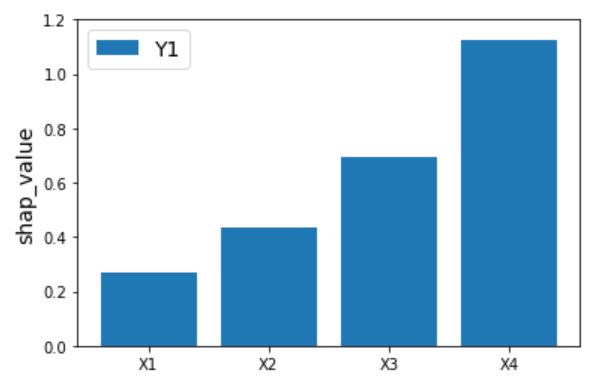
★Y2に対する寄与度分析の結果
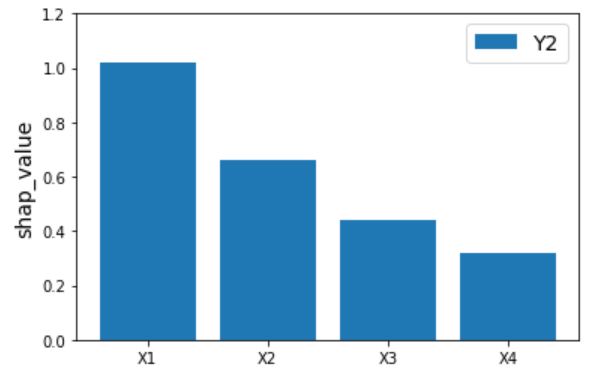
問題なく結果が出力できていそうですね。
shapの機能を使っても良いですが、内部で何を計算しているかを理解しておけば、こんな感じでどんなグラフ描写も可能になります。
おわりに
というわけで今回は複数の出力を持つモデルに対してshapを適用し、各出力ごとの入力の寄与度を分析⇒出力する方法をご紹介しました。
データ分析の際などにぜひご活用ください。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント