
こんにちは、ヒガシです。
先日業務中にガウシアンノイズを加えることで、なんたらかんたら・・・という報告を受けました。
ガウシアンノイズについては、おおまかなことは理解しているものの実際にどのようなことを行っているかを正確に把握することができていませんでした。
ということで今回はnumpyで実際にガウシアンノイズを作成してみようと思います。
私のようにこのあたりをなんとなくスルーしてきた人の参考になれば幸いです。
それではさっそくやっておきましょう!
ガウス分布とは
そもそもガウシアンノイズを理解するうえではガウス分布を理解する必要があります。
ガウス分布とは、ある統計量の分布をグラフ化したときに、そのグラフが左右対称であり、ピークが一つしかない分布のことを指します。
つまり絵にすると、以下のような形の分布がガウス分布であり
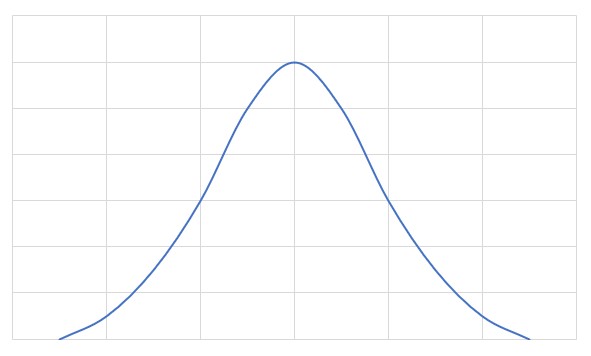
こんなのとか、
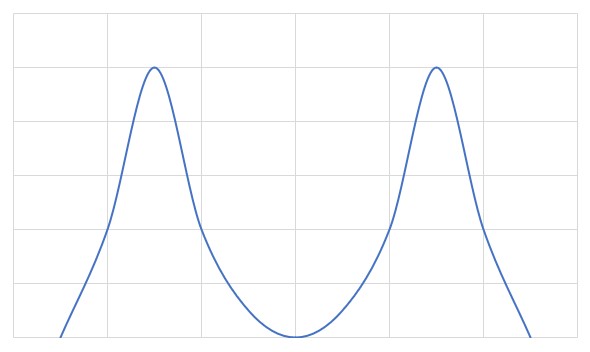
こんなのはガウス分布ではありません。
分散についての説明
とはいえ、左右対称でピークが1つ、なんて分布はいくらでも作れますよね。
要はこの条件を満たしていれば幅がものすごく広くても良いし、狭くても良いわけです。
この幅の広さを表す指標が分散というものです。
以下のグラフは分散が1の時と3の時のガウスを示したものです。
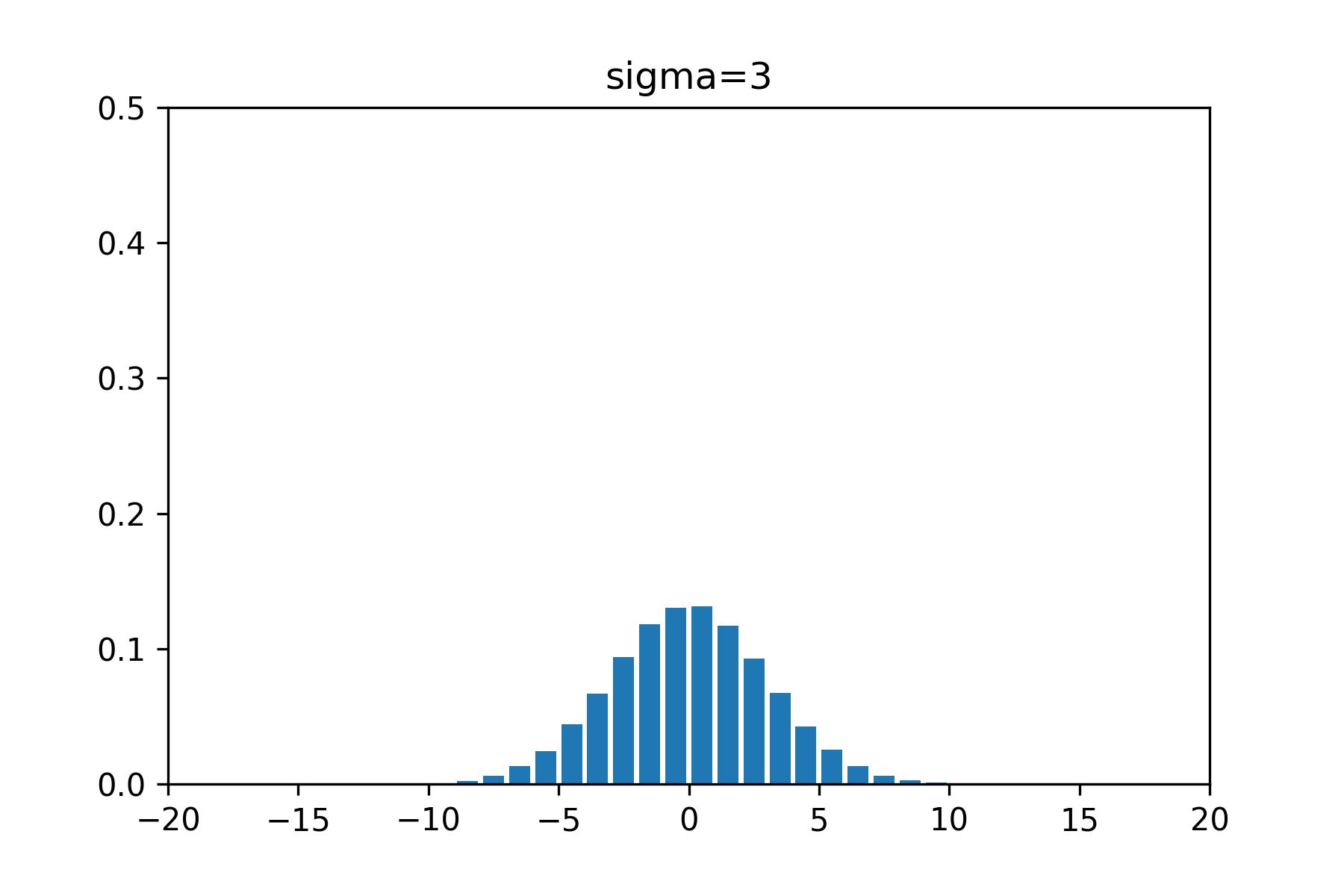
分散が大きいほうが、分布の幅が広くなっていることがわかると思います。
こんな形で同じガウス分布でも形の違いを表現することができるのです。
ガウシアンノイズとは
ガウス分布が理解できたところで、次はガウシアンノイズの説明に入ります。
ガウシアンノイズとは、ガウス分布に従う確率で発生するノイズだと理解すればよいです。
先ほどの分散が3の分布を例に説明します。

この分布に従うノイズを作成した例が以下になります。
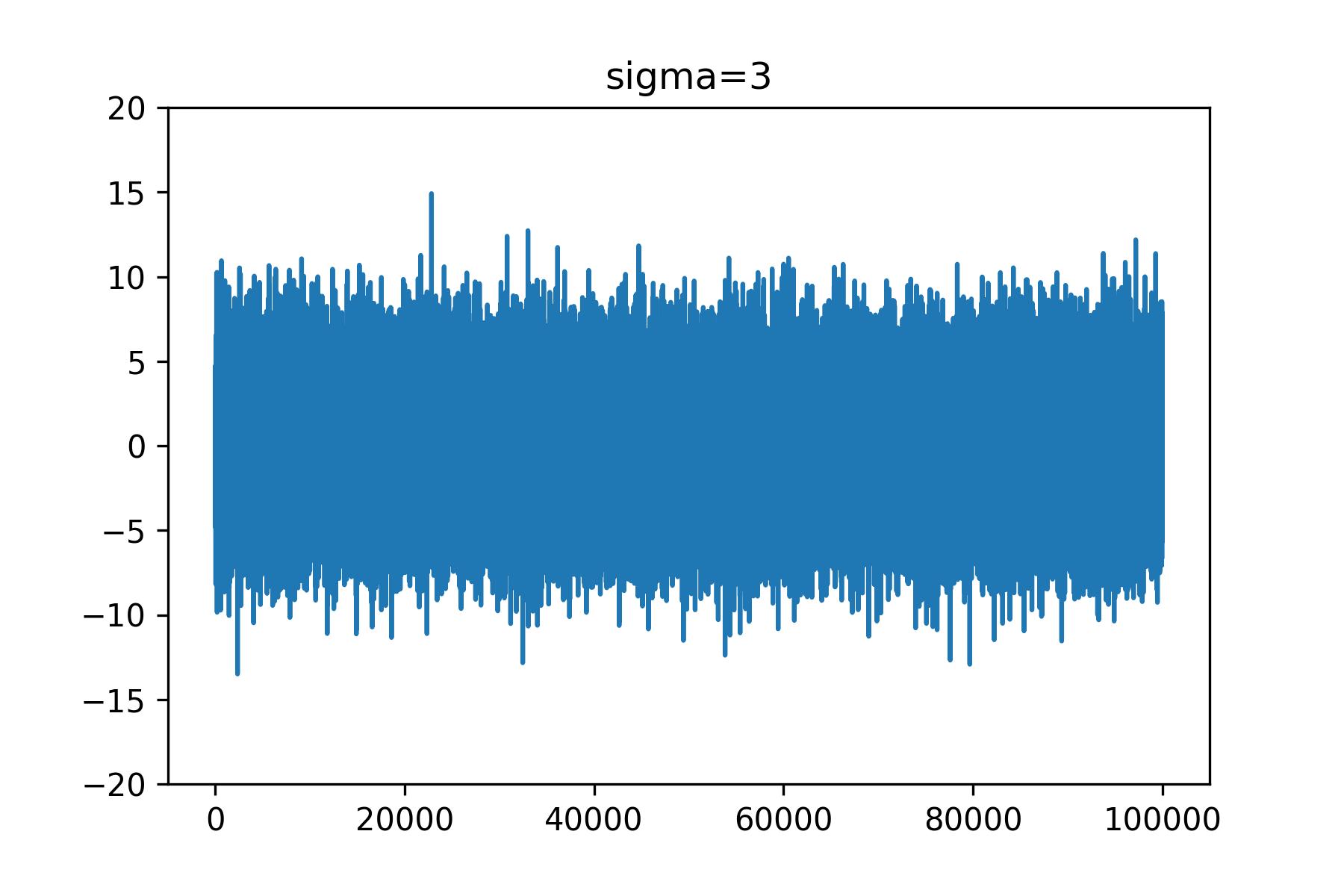
数が多すぎてよくわからないので、左端の方が拡大してみます。
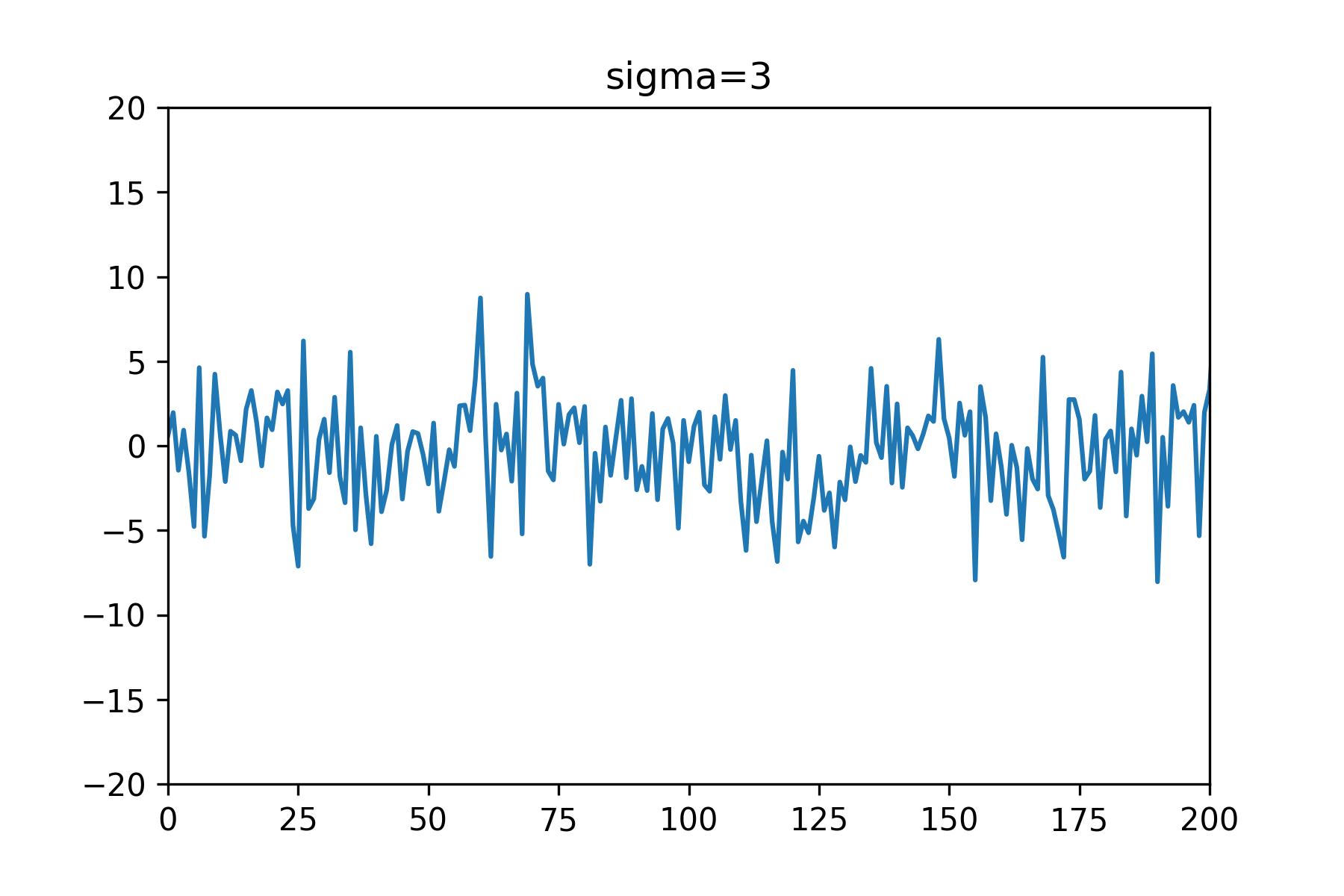
このギザギザの範囲を見ていただくと、ほとんどがー5から5の間に収まっていることがわかると思います。
そしてほんの一部だけが10付近まで伸びていることもわかると思います。
あらためてガウス分布をみてみましょう。

この分布は横軸がノイズの大きさ、縦軸がそのノイズが発生する確率を示しています。
ですので、-5~5の間のノイズが大量に発生し、そこを超えるノイズは稀に発生するというわけです。
numpyでガウシアンノイズを作成するサンプルコード
ガウシアンノイズを理解したところで、実際にnumpyを使ってガウシアンノイズを作成してみましょう。
ガウシアンノイズはnumpyのrandom.normalという方法で作成できます。
以下がそのサンプルコードです。
import matplotlib.pyplot as plt
import numpy as np
#データ作成
i = 100000
array = np.zeros(i)
sigma = 3
noise = np.random.normal(0, sigma, i)
#binの作成
bins = []
for k in range(-20, 20):
bins.append(k)
#ヒストグラムの作成
hist, bins = np.histogram(noise, bins=bins)
#グラフ用にbinの修正
X = []
for j in range(1, len(bins)):
X.append((bins[j - 1]+bins[j]) / 2)
#ヒストグラムのグラフ作成
hist_nor = hist / i
plt.bar(X, hist_nor)
plt.xlim(-20, 20)
plt.ylim(0, 0.5)
plt.title('sigma=' + str(sigma))
plt.savefig('hist_sigma=' + str(sigma) + '.jpg',dpi = 300)
plt.show()
plt.plot(array+ noise)
plt.title('sigma=' + str(sigma))
plt.ylim(-20, 20)
plt.xlim(0, 200)
plt.savefig('plot_sigma2=' + str(sigma) + '.jpg',dpi = 300)
plt.show()
7行目のsigmaが分散を表す変数です。
ここを変更すれば分散を変更したガウス分布、ガウシアンノイズを確認することができます。
分散を変更して実演
最後は実際に分散を振ってプログラムを実行してみましょう。
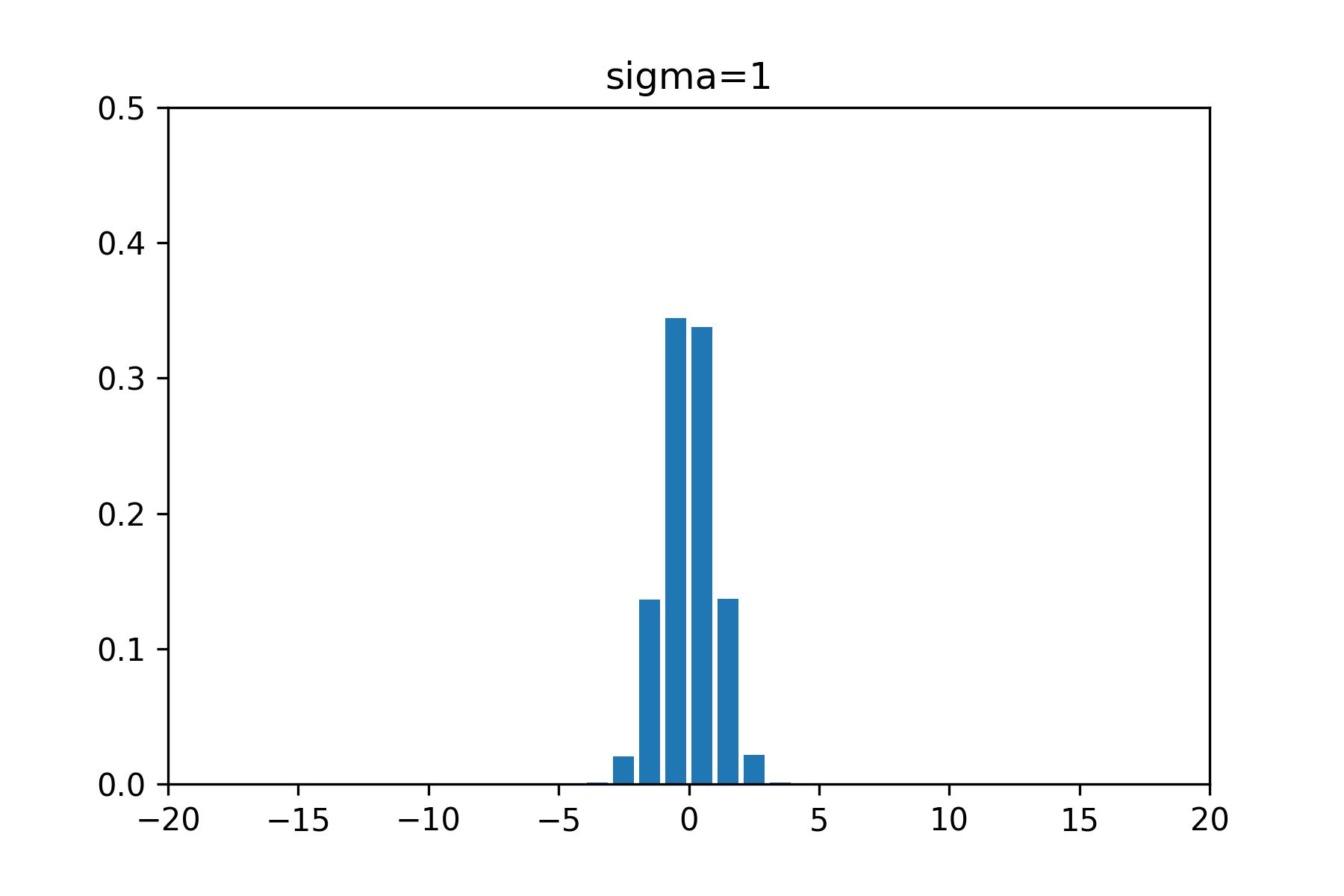
まずは分散が1の場合のヒストグラムとノイズです。
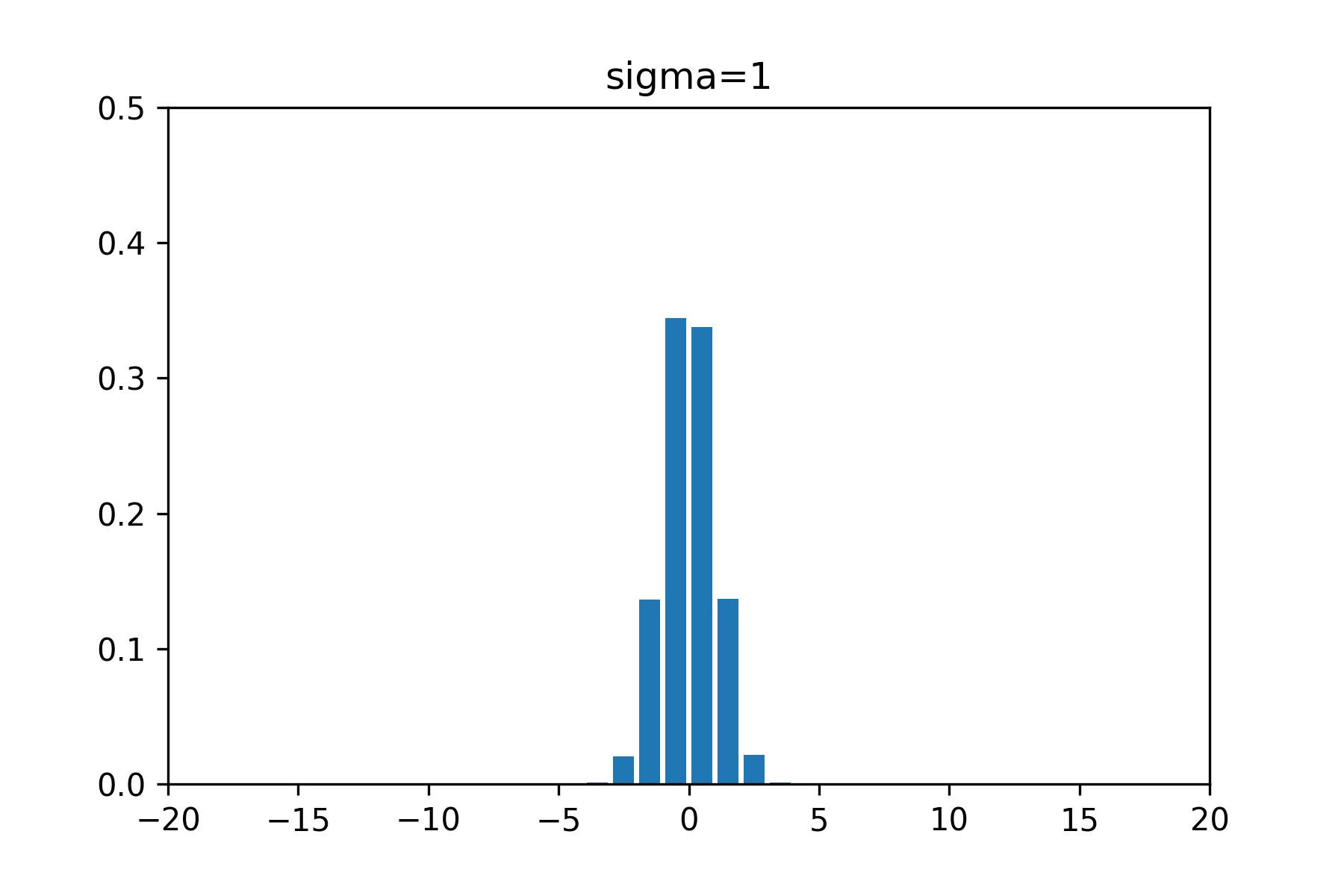
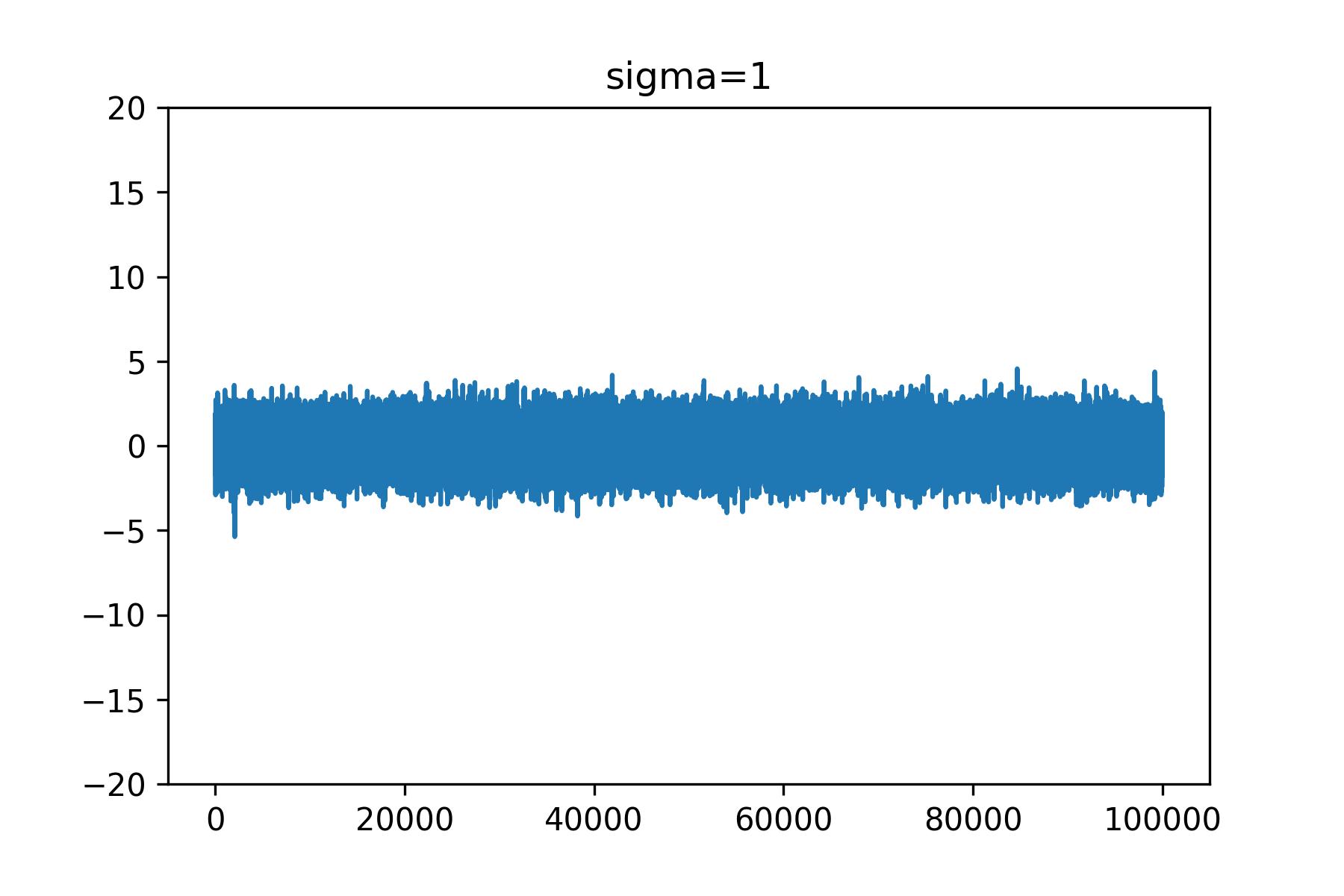
ノイズのギザギザの範囲とヒストグラムの棒グラフの範囲がだいたい一致していることがわかると思います。
次は分散が5の場合です。
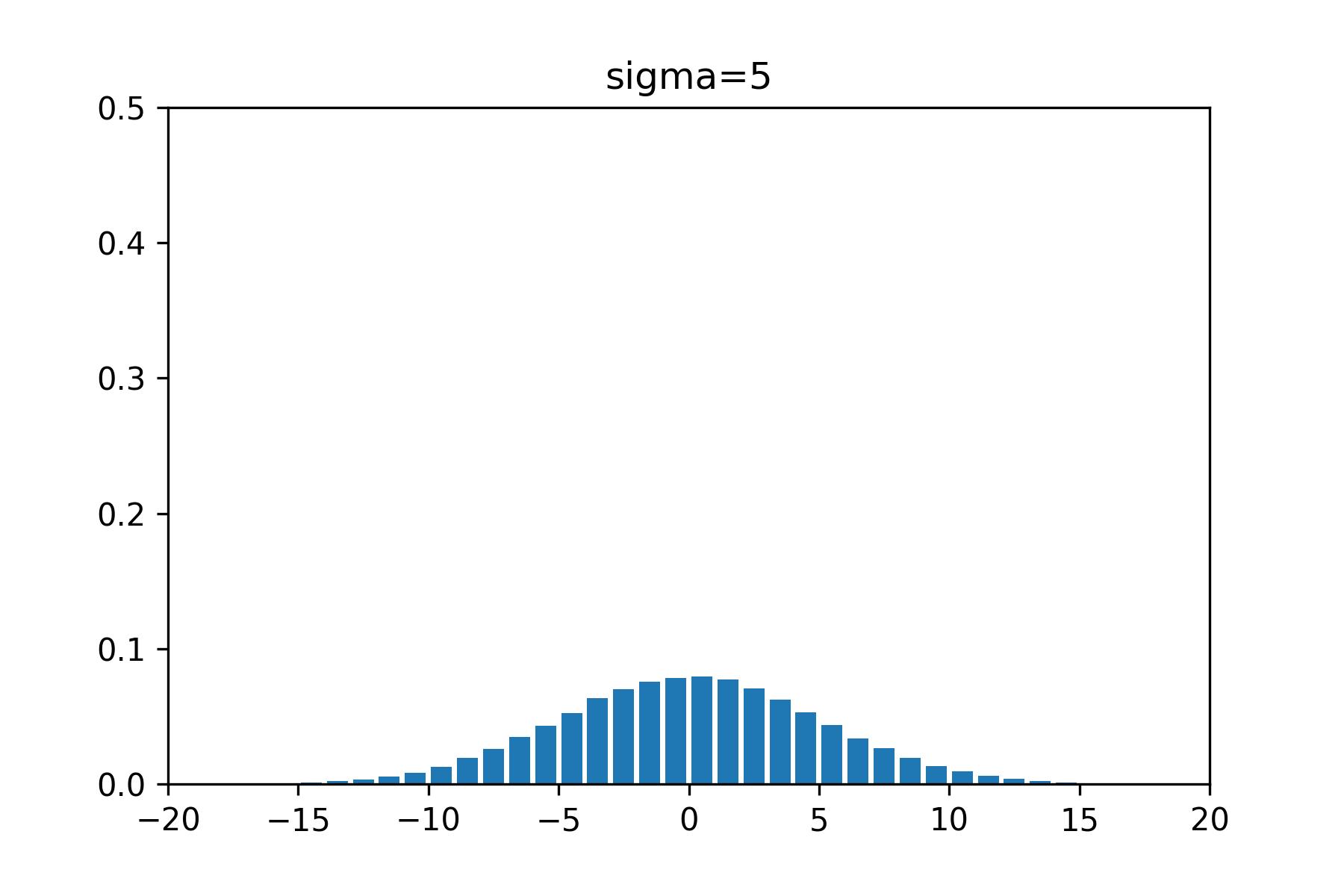
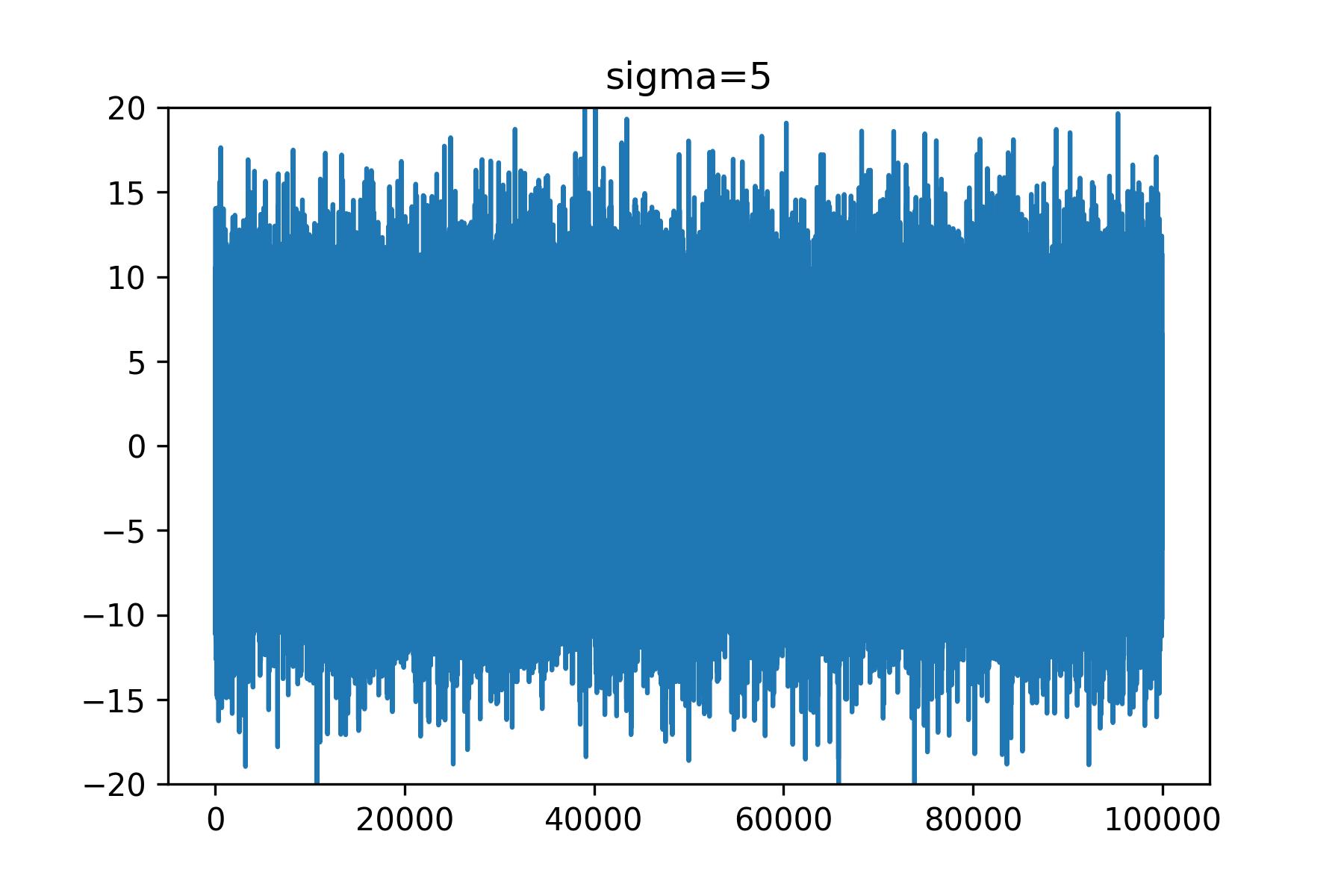
かなりノイズが広がりましたね。
こんな感じで分散を変更すれば自由にノイズの大きさをコントロールできるわけです。
おわりに
ということで今回はnumpyを使ったガウシアンノイズを実際に作成してみました。
AIの世界では準備したデータにこのようなノイズを加えることによって過学習を防いだりすることができます。
ぜひ覚えておきましょう。
このブログでは、このようなPythonスキルを多数紹介しています。
ぜひ他のページもご覧ください。
それではまた!




コメント