【Python-numpy】二次曲線近似式の係数を一発算出する方法！

こんにちは、ヒガシです。

このページではPython上で、以下のような二次曲線の近似式の係数３つを一発算出する方法をご紹介していきます。

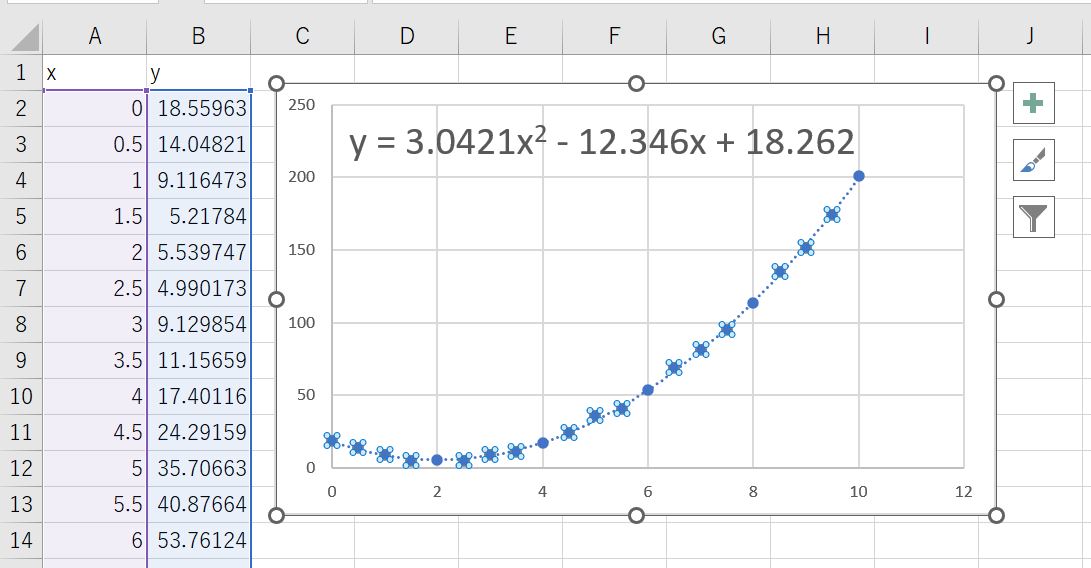
要は上記の近似式内のa=3.0421, b=-12.346, c=18.262という数値を算出していきます。

たったの１行のコードで算出可能ですので、ぜひ覚えておきましょう。

それではさっそくやっていきましょう。

二次曲線近似の係数を算出する方法
二次曲線近似式の実際の算出例
numpy.polyfitで二次曲線近似式を算出した結果
おわりに

二次曲線近似の係数を算出する方法

今回は二次曲線近似式の算出には、numpyのpolyfitというスキルを使用します。

使い方は以下の通りです。

import numpy as np
a,b,c=np.polyfit(x,y,2)

これで、二次曲線近似式(y=ax^2+bx+c)におけるa,b,cが算出できます。

超簡単ですね。

二次曲線近似式の実際の算出例

とはいえ、先ほどの例だけではよくわからないと思いますので、実際のデータを使って適用してみましょう。

使用するデータは冒頭でもお見せした以下のデータです。

このx,yをcsv化して保存してあります。

という状況で実際にnumpy.polyfitを使ってみましょう。

#ライブラリインポート
import numpy as np
import pandas as pd
#データの読み込み
data=pd.read_csv('sample_data.csv').values
x=data[:,0]
y=data[:,1]
#近似式の係数算出
a,b,c=np.polyfit(x,y,2)
#計算結果の確認
print('a='+str(round(a,3)))
print('b='+str(round(b,3)))
print('c='+str(round(c,3)))

４～７行目で先ほど紹介したデータを読み込み、９行目でnumpy.polyfitを実際に適用しています。