“Python” Calculate Distance of Two Points. How to Use numpy.linalg.norm

This page introduces how to calculate the distance of two points by using python & numpy.

It is called Euclidean distance mathematically.

 

So, let’s get started!!

 

How to Calculate the Distance of Two Points

It is not bad to calculate by using “pythagorean theorem” from coordinate of two points.

But there is more easy method.

The method is below.

You can use any dimension.

 

This time I introduce sample program of it at 2 and 3 dimension.

 

Sample Program at 2 Dimension

At first I introduce by using 2 dimension coordinate.

I use below two point.

(x,y)=(1,2) & (2,3)

 

You can calculate the distance of these points is 1.41421356… by using pythagorean theorem.

 

Let’s confirm this result by using “np.linalg.norm”

 

The sample program is below.

import numpy as np
a=np.array([1,2])
b=np.array([2,3])
distance=np.linalg.norm(b-a)
print(distance)

Of course not only (b-a) but also (a-b) is no problem.

 

The result is below.

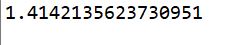
I think no problem about calculation.

 

Sample Program at 3 Dimension

Next, I introduce by using 3 dimension coordinate.

I use below two point.

(x,y,z)=(1,2,3) & (2,3,4)

 

You can calculate the distance of these points is 1.7320508… by using pythagorean theorem.

 

Let’s confirm this result by using “np.linalg.norm”

 

The sample program is below.

import numpy as np
a=np.array([1,2,3])
b=np.array([2,3,4])
distance=np.linalg.norm(b-a)
print(distance)

Of course not only (b-a) but also (a-b) is no problem.

 

The result is below.

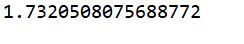
I think it is also no problem about calculation.

 

That’s all. Thank you!!