
こんにちは、ヒガシです。
このページではPythonを使って、以下の画像に示すように平面上にある2直線の交点座標を算出する方法をご紹介していきます。
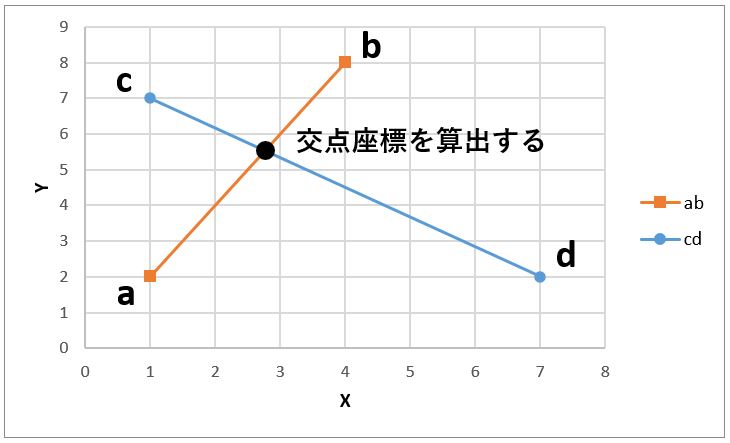
あなたがやることは各直線を構成する4点a,b,c,dのX,Y座標を指定するだけでOKです。
それではさっそくやっていきましょう!
2直線の交点座標を算出する方法の解説
まずはどうやって2直線の交点を算出するか説明していきます。
やることはいたってシンプルです。
まずは以下の画像に示すように2つの直線上それぞれに点P,Qを適当に取り、その2点を結ぶ線分PQの長さを計測します。
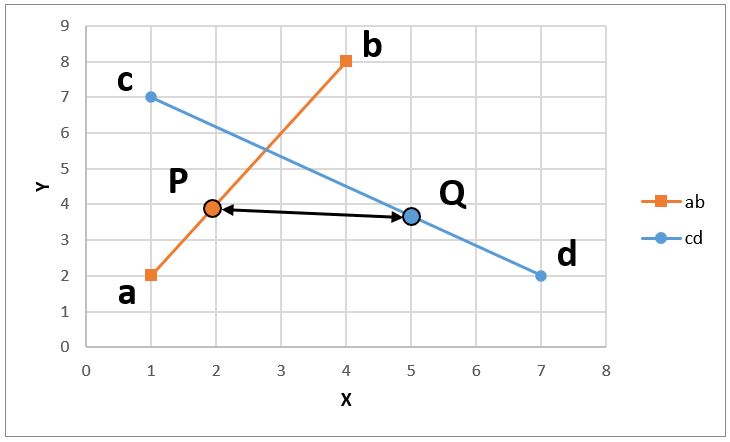
この作業をP,Qの位置を網羅的に変更しながら実施し、線分PQの長さが最小になるP,Qの座標を探索していきます。
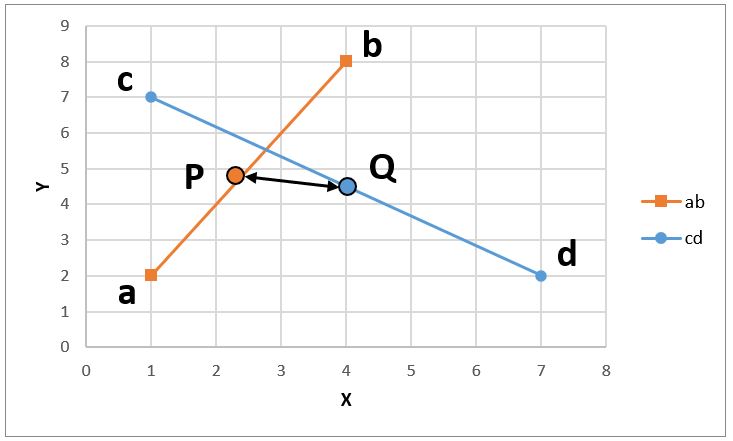
※うまく計算できれば最終的にP,Qの座標は一致することになります。
手計算でやればもっと数学的に説くことは可能ですが、コンピューターはそういった計算は得意ではないので、上記で説明したような探索的な計算で解いていきます。
この作業をプログラミング言語「Python」を使って実行していきます。
2直線を構成する4点の座標を指定する
交点を計算する上で、まずは2つの直線がなければ話になりません。
というわけでまずは2つの直線を構成する4点の座標を指定してあげましょう。
今回は以下のように指定してあげました。
a=[1,2]
b=[4,8]
c=[1,7]
d=[7,2]
エクセルでグラフを書くとこんな感じですね。
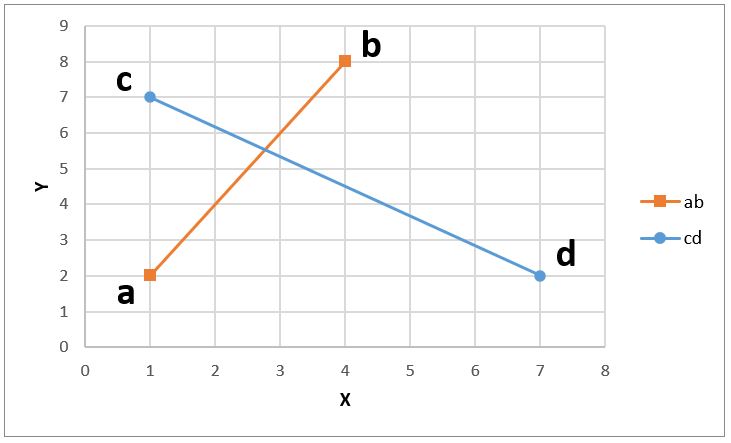
グラフを見てわかるとおり、交点はX=2~3, Y=5~6の間にありますね。
以降では、この交点の詳細座標を探索的に計算していきます。
2直線の交点を算出するサンプルコード
それでは前置きはこのくらいにして、先ほど指定して2直線の交点を求めるプログラムを書いていきましょう。
以下がそのコードです。
#ライブラリインポート
import numpy as np
#ab,cdでそれぞれ繋がる2直線の最短距離を計算する
a=[1,2]
b=[4,8]
c=[1,7]
d=[7,2]
line1=[a,b]
line2=[c,d]
a,b=line1[0],line1[1]
c,d=line2[0],line2[1]
ABbec=np.array([b[0]-a[0],b[1]-a[1]])
CDbec=np.array([d[0]-c[0],d[1]-c[1]])
#2直線の距離を計算する関数
def calc_distance(s,t):
PQbec=(c+CDbec*s)-(a+ABbec*t)
distance=np.linalg.norm(PQbec)
return distance
def calc_pos(s,t):
Qpos=(c+CDbec*s)
Ppos=(a+ABbec*t)
return Ppos,Qpos
#2直線の距離を探索する関数
def make_map(ss,tt):
z_list=[]
ij_list=[]
st_list=[]
for i in range(len(ss)):
for j in range(len(tt)):
s,t=ss[i],tt[j]
z=calc_distance(s,t)
z_list.append(z)
ij_list.append([i,j])
st_list.append([s,t])
return z_list,ij_list,st_list
#大きな範囲で最小値をざっくり探索
ini_max=2000
ini_min=-2000
delta=200
num_search=7
ss=np.linspace(ini_min,ini_max,delta)
tt=np.linspace(ini_min,ini_max,delta)
z,ij,st=make_map(ss,tt)
min_val=np.amin(np.array(z))
min_index=z.index(min_val)
#範囲を狭めながら最小値を繰り返し計算
minz_list=[]
for k in range(num_search):
i,j=ij[min_index][0],ij[min_index][1]
smax,smin=min(ss[i+2],ini_max),max(ss[i-2],ini_min)
tmax,tmin=min(tt[j+2],ini_max),max(tt[j-2],ini_min)
ss=np.linspace(smin,smax,delta)
tt=np.linspace(tmin,tmax,delta)
z,ij,st=make_map(ss,tt)
min_val=np.amin(np.array(z))
min_index=z.index(min_val)
minz_list.append(min_val)
Ppos,Qpos=calc_pos(st[min_index][0],st[min_index][1])
print('Ppos=')
print(Ppos)
print('Qpos=')
print(Qpos)
print('mean_pos=')
print((Qpos+Ppos)/2)
先ほども説明した通り、今回は探索的に交点座標を求めていきます。
そのため探索範囲はあらかじめ指定しておく必要があります。
それを行っているのが、42,43行目です。(ini_max、ini_min)
もしこの指定範囲内に解がなければ正しい値を求めることはできませんのでなるべく広範囲を指定しておく必要があります。
ただし、広範囲すぎると探索が粗くなりますので9行目の探索の細かさ(delta)を大きくするか探索回数(num_search)を大きくする必要がでてきます。
しかしながらこれらの数値は大きくすればするほど計算時間はかかってしまいますのでその点はご注意ください。
サンプルコードの実行結果確認
それでは先ほどのサンプルコードを実行してみましょう。

いざ、実行!!!
※少し時間がかかります。
計算が終わると以下の結果が算出されました。
これが探索に使った点P、点Qの座標、およびその中心座標です。

冒頭に説明した通り、今回はそれぞれの線上をP,Qという2点を動かしながら探索していきます。

最終的に交点座標にたどり着いた場合、P,Qの座標は一致しているはずです。
もし一致していなければ探索がうまくいっていないので、先ほど紹介したパラメータを調整して再度計算してみることをオススメします。
とりあえず今回は問題なくグラフの交点付近を算出できていそうですね。
おわりに
というわけで今回はpythonを使って、平面上にある2直線の交点座標を算出する方法をご紹介しました。
空間設計の際などにぜひご活用ください。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント