
こんにちは、ヒガシです。
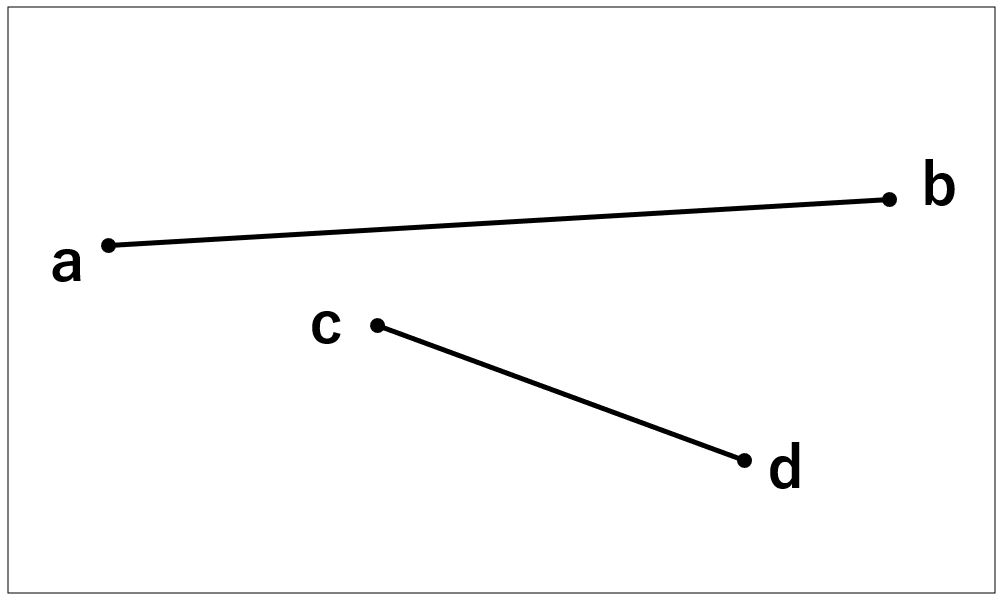
このページでは以下の画像に示すように、ねじれの位置にある2直線の最近点座標、および最短距離を算出する方法をご紹介していきます。
◆2直線の最近点座標のイメージ図
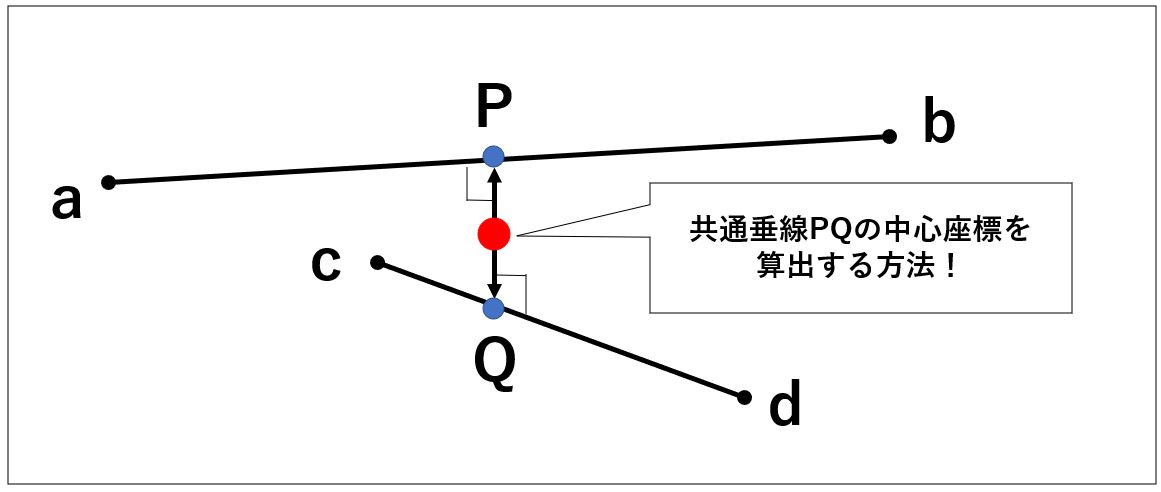
◆2直線の最短距離のイメージ図
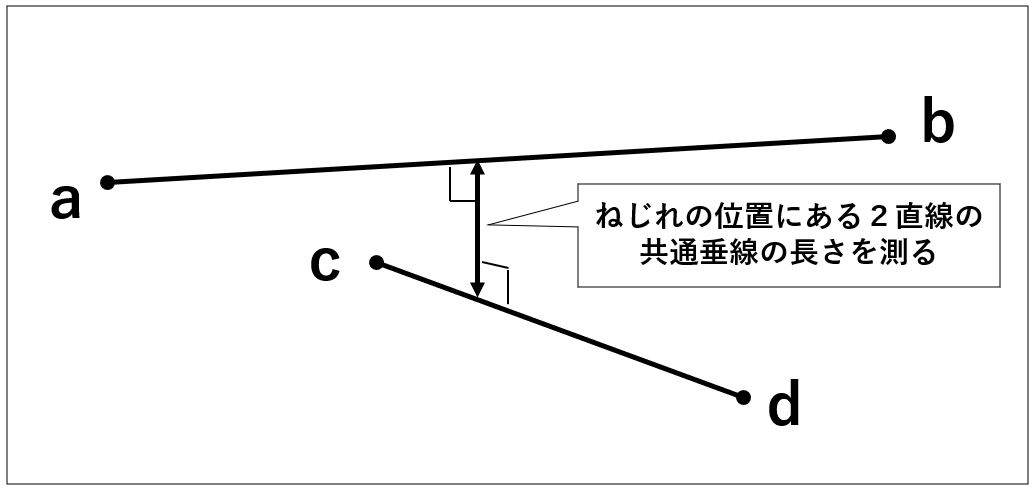
あなたが指定することは、上図のa,b,c,d各点の座標を指定してあげるだけでOKです。
座標、距離の算出方法の解説
まず始めに、今回求めたい数値は数学的にまじめに計算していけば手計算でも容易に求めることは可能です。
そのやり方は以下で詳細解説されていますので、こちらをご覧ください。

しかしながら、このページを見ている方は、

手計算でやってる暇はない。コンピューターにやってほしい。
と思っていることでしょう。
しかしながらコンピューターにとってこういった計算を数学的に実行していくのはあまり得意ではありません。
というわけで今回はエクセルVBAを使って多くの計算を実施し、探索的に解を求めていきます。
イメージ的には以下の通りです。
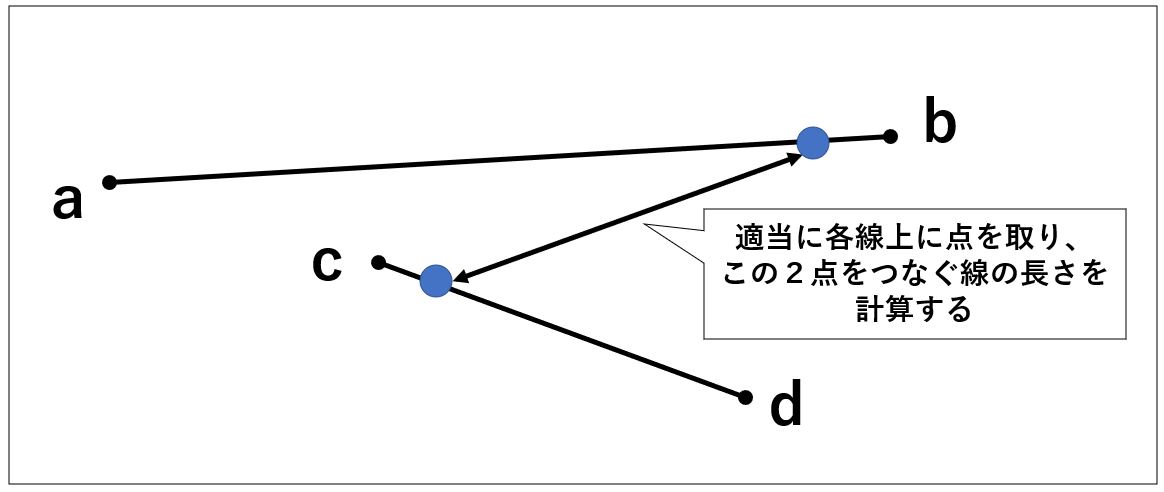
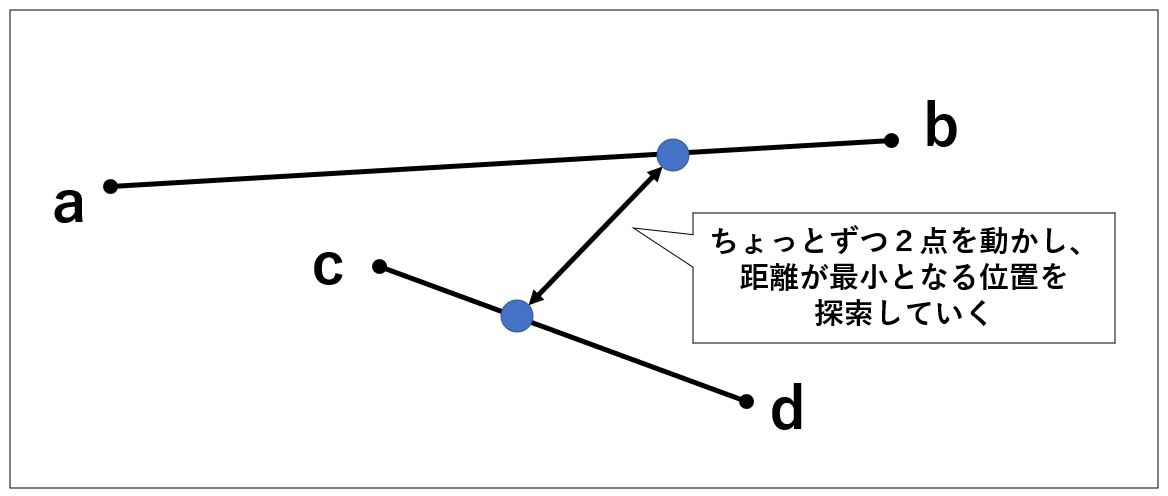
最短距離が見つかったら、その距離を取る2点の中心座標をもとめる。
これで今回求めたい「ねじれの位置にある2直線の最近点座標、および最短距離」を算出することができますね。
エクセルVBAの実行環境を整える
本題に入る前に、今回は先ほど紹介した計算をエクセルVBAを使って実行していきます。
VBAを使ったことがない、という方は以下でやり方を解説していますので、まずはこちらからご覧ください。
エクセルマクロ(VBA)の始め方!初心者向けに画像を使って詳細解説
2直線を構成する座標を指定する
計算を行うにあたって、まずは2直線の情報がなければ話になりません。
まずは以下のイメージ図を参考に2直線を構成するa,b,c,dの座標を指定してあげます。
これをエクセル上に記入します。
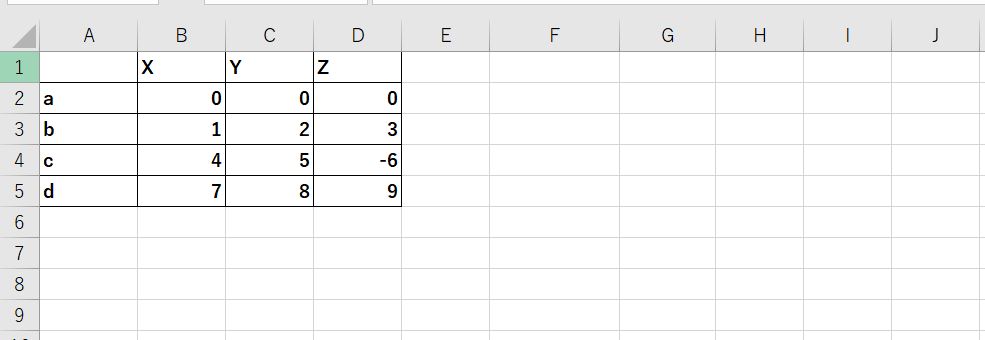
今回はこんな感じで指定しています。
なお、以降で紹介するプログラムは上記画像と同じセルに情報が記入されている前提で書いています。
修正は面倒だと思いますので、できれば上記の画像と同じセルに情報を記入してください。
また、計算の過程でその他のセルも使用します。
必ず新規シート上で実行するようにしてください。
2直線の最近点、最短距離を算出するサンプルコード
それでは事前準備はここまでです。
本題であるプログラムを記述していきましょう。
以下が今回求めたいねじれの位置にある2直線の最近点座標、および最短距離を算出するサンプルコードです。
Sub search_main()
Dim sea_delta As Integer
Dim num_search As Integer
Dim sea_max As Single, sea_min As Single
Call pre_set(1)
Application.ScreenUpdating = Flase
Range("K1:ZZ500").ClearContents
sea_max = 2000
sea_min = -2000
sea_delta = 20
num_search = 10
s_max = sea_max
t_max = sea_max
s_min = sea_min
t_min = sea_min
For k = 1 To num_search
Call draw_matrix_s(s_max, s_min, sea_delta)
Call draw_matrix_t(t_max, t_min, sea_delta)
Call search_L(s_max, s_min, t_max, t_min, sea_delta)
st = search_index(sea_delta)
s_max = st(0)
s_min = st(1)
t_max = st(2)
t_min = st(3)
Next
Range("K1:ZZ500").ClearContents
End Sub
Sub pre_set(a)
Range("A1:I8").Font.Bold = True
Range("A7:B8").Borders.Weight = xlThin
Range("F1:I3").Borders.Weight = xlThin
Range("F5:G5").Borders.Weight = xlThin
Range("F7:I8").Borders.Weight = xlThin
Range("A7") = "s"
Range("A8") = "t"
Range("G1") = "X"
Range("H1") = "Y"
Range("I1") = "Z"
Range("F2") = "P"
Range("F3") = "Q"
Range("F5") = "PQ_Distance"
Range("F8") = "PQ_Center"
Range("G7") = "X"
Range("H7") = "Y"
Range("I7") = "Z"
Range("G2") = "=(B3-B2)*$B$7+B2"
Range("H2") = "=(C3-C2)*$B$7+C2"
Range("I2") = "=(D3-D2)*$B$7+D2"
Range("G3") = "=(B5-B4)*$B$8+B4"
Range("H3") = "=(C5-C4)*$B$8+C4"
Range("I3") = "=(D5-D4)*$B$8+D4"
Range("G5") = "=SQRT((G3-G2)^2+(H3-H2)^2+(I3-I2)^2)"
Range("G8") = "=(G2+G3)/2"
Range("H8") = "=(H2+H3)/2"
Range("I8") = "=(I2+I3)/2"
End Sub
Sub draw_matrix_s(sea_max, sea_min, sea_delta)
For i = 0 To sea_delta
Cells(2 + i, 11) = sea_min + (sea_max - sea_min) / sea_delta * i
Next
End Sub
Sub draw_matrix_t(sea_max, sea_min, sea_delta)
For i = 0 To sea_delta
Cells(1, 12 + i) = sea_min + (sea_max - sea_min) / sea_delta * i
Next
End Sub
Sub search_L(s_max, s_min, t_max, t_min, sea_delta)
For ss = 0 To sea_delta
s = Cells(2 + ss, 11)
For tt = 0 To sea_delta
t = Cells(1, 12 + tt)
Range("B7") = s
Range("B8") = t
Cells(2 + ss, 12 + tt) = Range("G5")
Next
Next
End Sub
Function search_index(sea_delta)
Dim return_val(3) As Single
data_array = Range(Cells(2, 12), Cells(2 + sea_delta, 12 + sea_delta))
min_value = Application.WorksheetFunction.Min(data_array)
For i = 1 To UBound(data_array, 1)
For j = 1 To UBound(data_array, 2)
If data_array(i, j) = min_value Then
max_r = Application.WorksheetFunction.Min(1 + i + 2, 2 + sea_delta)
min_r = Application.WorksheetFunction.Max(1 + i - 2, 2)
max_c = Application.WorksheetFunction.Min(11 + j + 2, 12 + sea_delta)
min_c = Application.WorksheetFunction.Max(11 + j - 2, 12)
s_max = Cells(max_r, 11) + Cells(max_r, 11) - Cells(max_r - 2, 11)
s_min = Cells(min_r, 11) - (Cells(min_r + 2, 11) - Cells(min_r, 11))
t_max = Cells(1, max_c) + Cells(1, max_c) - Cells(1, max_c - 2)
t_min = Cells(1, min_c) - (Cells(1, max_c + 2) - Cells(1, max_c))
End If
Next
Next
return_val(0) = s_max
return_val(1) = s_min
return_val(2) = t_max
return_val(3) = t_min
search_index = return_val
End Function
先ほど、「網羅的な計算を実施し、探索的に解を求める」という説明をしたと思います。
なので探索範囲はあなたが指定する必要があります。
それを指定しているのが7、8行目です。(sea_max、sea_min)
もしこの指定範囲内に解がなければ正しい値を求めることはできませんのでなるべく広範囲を指定しておく必要があります。
ただし、広範囲すぎると探索が粗くなりますので9行目の探索の細かさ(sea_delta)を大きくするか探索回数(num_search)を大きくする必要がでてきます。
しかしながらこれらの数値は大きくすればするほど計算時間はかかってしまいますのでその点はご注意ください。
サンプルコードの実行結果確認
それでは先ほどのサンプルコードを実行してみましょう。

いざ、実行!!!
※少し時間がかかります。
計算が終わると以下の結果が算出されました。
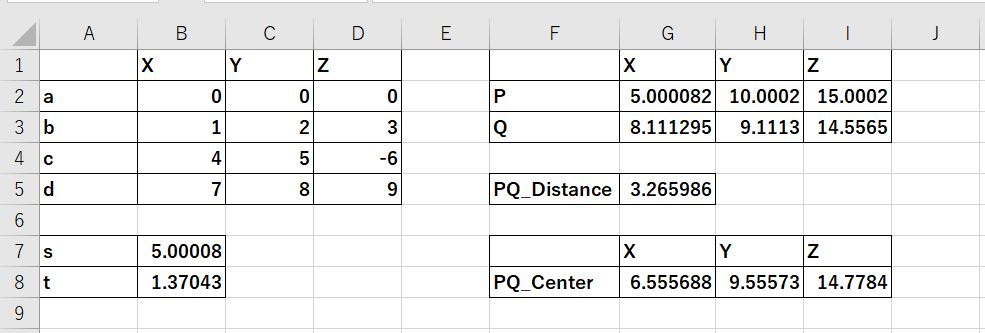
このPQ_Distanceが最短距離、PQ_Centerが最近点座標になります。
手計算で算出される答えとしては、
最短距離=3.2659863…
最近点=(6.555…, 9.555…, 14.777…)
ですのでほぼ近い値は計算できていますね。
まぁ探索的に求めるので多少のずれは仕方ないですね。
おわりに
というわけで今回は、エクセルVBAをつかってねじれの位置にある2直線の最短距離、最近点座標を求める方法をご紹介しました。
設計の際などにぜひご活用ください。
※あくまでも自己責任でお願いします。
このように、私のブログではエクセルスキルはもちろん、様々なプログラミングスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
それではまた!




コメント