
こんにちは、ヒガシです。
今回はPythonを使って、ねじれの位置にある2直線が最も接近する点(最近点)の座標を算出する方法をご紹介していきます。
つまり共通垂線の中心座標を算出するということですね。
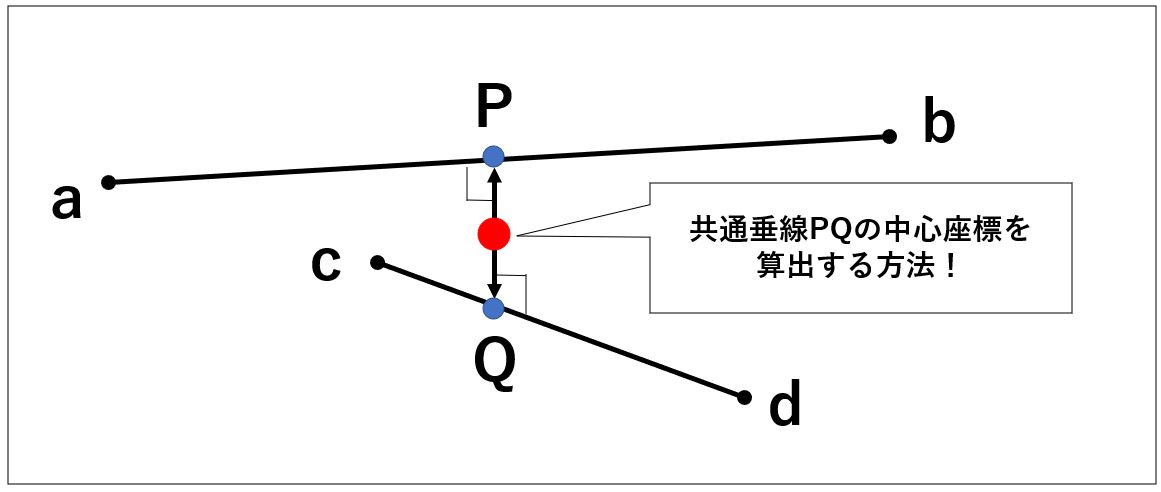
※前回の記事では、この共通垂線の長さを算出するプログラムをご紹介しています。今回もそのコードを流用していますので、興味があればまずは前回の記事からご覧ください。
【Python】ねじれの位置にある2直線の最短距離を計算する方法
共通垂線に関する参考サイトのご紹介
以下のサイトにて今回算出する内容を数学的に詳細解説してくれています。

今回はこの作業をPython上でやったらどんな感じかをご紹介していこうと思います。
ですので、サンプルコードで使う2つの直線の構成座標も上記サイトと同じものを流用させていただいております。
Pythonで2直線の最近点を算出するサンプルコード
それではさっそくですが、サンプルコードのご紹介です。
※先ほど紹介した参考サイトにて算出された正解データもあわせて表示するようにしてます。Python上で算出した結果はmean_pos=で表示されている部分です。
#ライブラリインポート
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#ab,cdでそれぞれ繋がる2直線の最短距離を計算する
#参照(https://math-juken.com/kijutu/kyoutusuisen/)
a=[0,0,0]
b=[1,2,3]
c=[4,5,-6]
d=[7,8,9]
line1=[a,b]
line2=[c,d]
a,b=line1[0],line1[1]
c,d=line2[0],line2[1]
ABbec=np.array([b[0]-a[0],b[1]-a[1],b[2]-a[2]])
CDbec=np.array([d[0]-c[0],d[1]-c[1],d[2]-c[2]])
#2直線の距離を計算する関数
def calc_distance(s,t):
PQbec=(c+CDbec*s)-(a+ABbec*t)
distance=np.linalg.norm(PQbec)
return distance
def calc_pos(s,t):
Qpos=(c+CDbec*s)
Ppos=(a+ABbec*t)
return Ppos,Qpos
#2直線の距離を探索する関数
def make_map(ss,tt):
z_list=[]
ij_list=[]
st_list=[]
for i in range(len(ss)):
for j in range(len(tt)):
s,t=ss[i],tt[j]
z=calc_distance(s,t)
z_list.append(z)
ij_list.append([i,j])
st_list.append([s,t])
return z_list,ij_list,st_list
#大きな範囲で最小値をざっくり探索
ini_max=2000
ini_min=-2000
delta=200
ss=np.linspace(ini_min,ini_max,delta)
tt=np.linspace(ini_min,ini_max,delta)
z,ij,st=make_map(ss,tt)
min_val=np.amin(np.array(z))
min_index=z.index(min_val)
#範囲を狭めながら最小値を繰り返し計算
minz_list=[]
for k in range(7):
i,j=ij[min_index][0],ij[min_index][1]
smax,smin=min(ss[i+2],ini_max),max(ss[i-2],ini_min)
tmax,tmin=min(tt[j+2],ini_max),max(tt[j-2],ini_min)
ss=np.linspace(smin,smax,delta)
tt=np.linspace(tmin,tmax,delta)
z,ij,st=make_map(ss,tt)
min_val=np.amin(np.array(z))
min_index=z.index(min_val)
minz_list.append(min_val)
Ppos,Qpos=calc_pos(st[min_index][0],st[min_index][1])
print('Ppos=')
print(Ppos)
print('Qpos=')
print(Qpos)
print('mean_pos=')
print((Qpos+Ppos)/2)
#正解データの計算(https://math-juken.com/kijutu/kyoutusuisen/)
P=np.array([5,10,15])
Q=np.array([73,82,131])/9
PQmean=(P+Q)/2
print('answer=' +str(PQmean))
基本的にやっていることは、
①2つの直線上に適当にそれぞれ点を一打ち、その2点をちょっとずつ動かして最接近する2点を探索
②その2点の平均座標=最接近する座標
というわけです。
前回記事で図解していますので、イメージがわかなければ前回記事をご覧ください。
【Python】ねじれの位置にある2直線の最短距離を計算する方法
サンプルコードの実行結果確認
それでは先ほど紹介したサンプルコードを実行してみましょう。
以下の結果が得られました。
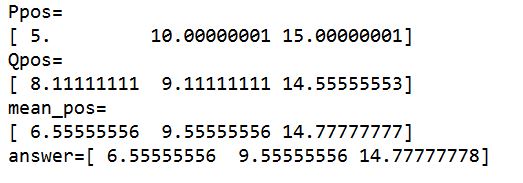
mean_pos=で表示されている部分が今回Pythonで算出した結果、answer=で表示されている部分が参考サイトにて導出されていた結果です。
上記のとおり微小なずれはありますが、ほぼ同じ結果になっていますね。
というわけで問題なく計算できていそうですね。
おわりに
というわけで今回はpythonを使って、ねじれの位置にある2直線の最近点を算出する方法をご紹介しました。
部品設計の際などにぜひご活用ください。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント