
こんにちは、メーカーエンジニアのヒガシです。
強化学習を勉強していると、
「エージェントはこの環境下において最も得られる報酬の期待値が大きい行動を取る・・・」
といった説明をよく目にするのではないでしょうか?
今回はこの期待値に関する話をしていきます。
そもそも期待値とは?
まずは期待値について解説していきましょう。
これは高校数学でも習った期待値とまったく同じ意味で、どのような結果が期待できるかを表す数値です。
例えば以下のように1~10までのカードが入った箱から適当に1枚のカードを取り出すという問題を考えてみましょう。
この場合の期待値はいくつでしょうか?
高校で習ったことをそのまま適用すると以下の式で算出可能なはずです。
期待値=(1+2+3+4+5+6+7+8+9+10)/10
計算結果は5.5になるはずです。
これがこの問題での期待値ですね。
同様に4~8までのカードが入った箱から適当に1枚のカードを取り出すという問題を考えてみましょう。
この場合、
期待値=(4+5+6+7+8)/5
計算結果は6.0になるはずです。
これがこの問題での期待値ですね。
例えば、上記の2つの問題に対して
〇どちらか一方の箱からカードを取らないといけない
〇取り出したカードの数字の大きさ分のお金をゲットできる
という状況があった場合、どちらの箱からカードを取るでしょうか?
迷わず2つめの5枚のカードが入った箱を選ぶと思います。
なぜならそちらの方が期待値が大きいことがわかっているからですよね。
しかしながら、中身がわからない未知の箱の場合、どちらの箱から取るのが最も得られる金額の期待値が大きいのかわからないですよね?
わからないから試行錯誤してどんな金額が得られそうか(つまり期待値)、を学習していく、これが強化学習です。
(ものすごくざっくり説明するとですが)
では試行錯誤しながら期待値を学習していく、とはどうゆうことをやっているのでしょうか?
これが今回の記事の本題です。
未知の問題に対して試行錯誤しながら期待値を計算する方法
先ほどの例と同様に以下の1~10までのカードが入った箱から1枚のカードを取り出す例で考えていきましょう。

中身がわかっている状態であれば、この問題の期待値は5.5でしたよね。
この5.5という数値を試行錯誤だけで求めていってみましょう。
というわけで試行錯誤しながら期待値を求めるには、以下の式を使います。
いきなり数式がでてきて驚かれているひとも多いとおもいますが、いったんはこんな式で何度も計算していけば、期待値を出せる、という風に受け入れてください。
以降で紹介するプログラムと結果を見ればなんとなく理解できるはずです。
それでは、ここからは実際にプログラムを書きながら実演してみます。
以下がそのプログラムです。
※Pythonで実装しています。
#ライブラリインポート
import random
import numpy as np
import matplotlib.pyplot as plt
#期待値を算出する
E=0
lr=0.001
trial_number=6000
E_history=[]
for i in range(trial_number):
#1~10までの数字をランダムに出す
rnd=random.randint(1,10)
#出た結果をもとに期待値を更新する(記事中の式を使用)
E=E*(1-lr)+rnd*lr
#グラフ作成用にデータを保存
E_history.append(E)
#グラフの描写
x=np.linspace(1,len(E_history),len(E_history))
plt.plot(x, E_history, label='E_histpry')
plt.plot([0,trial_number],[5.5,5.5], label='Theoretical value')
plt.legend(loc='lower right', fontsize=14)
plt.xlabel('Trial_Number',fontsize=14)
plt.ylabel('Expected_Value',fontsize=14)
plt.title('lr='+str(lr))
plt.ylim(0, 10)
plt.savefig('lr='+str(lr)+".jpg", dpi=300)
今回は試行回数(trial_number)6000回、学習率(lr)は0.001で実行しています。
このプログラムを実行すると以下の画像が出力されました。
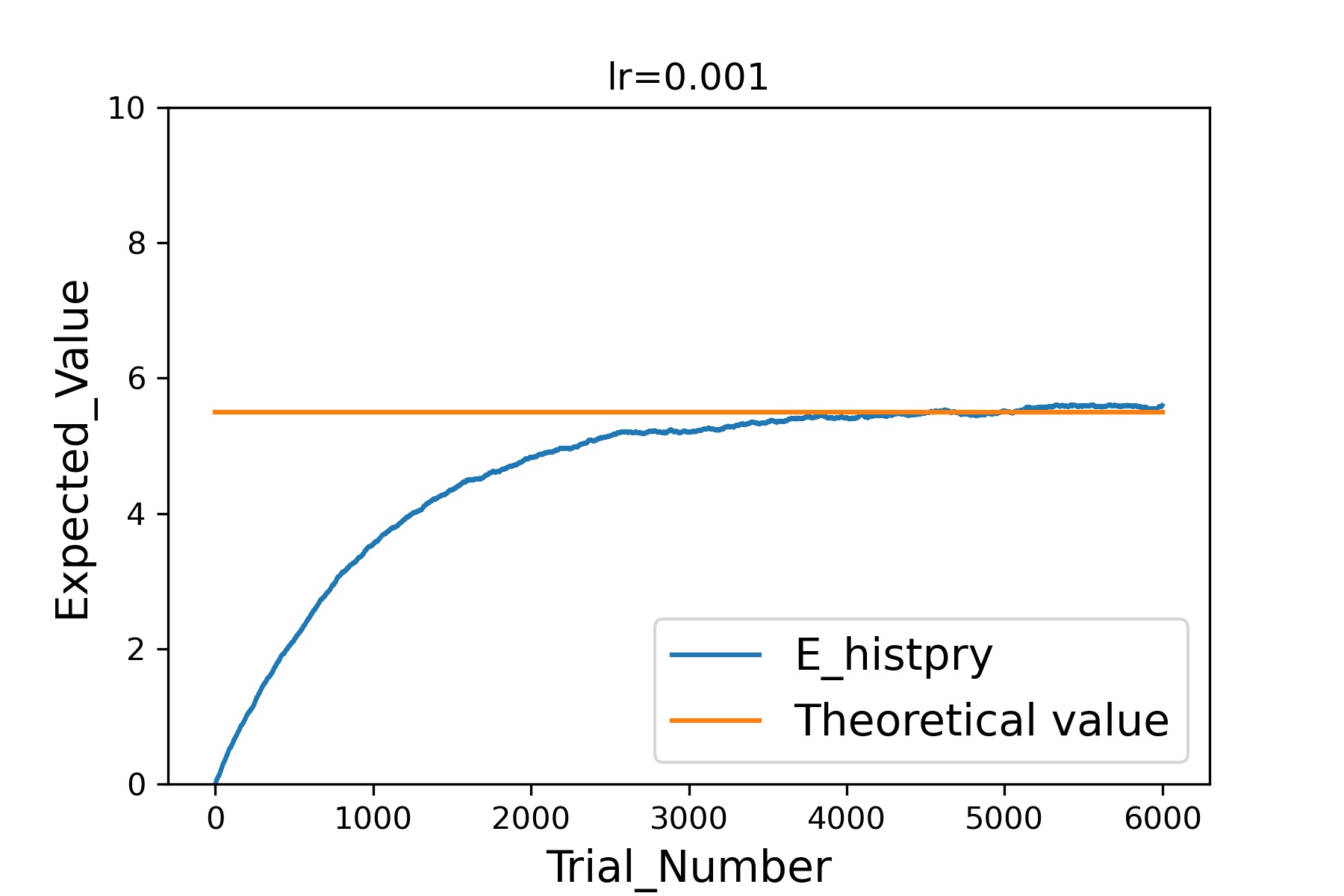
このグラフの横軸は試行回数、縦軸は期待値です。
青線が先ほど紹介した式で算出した各試行回数における期待値の結果、オレンジ線はどんな数字が出るかがわかっていると想定して算出した理論上の期待値(先ほど算出した5.5という数値)です。
このように試行回数を重ねるごとに、算出される期待値は理論上の期待値(5.5)にどんどん近づき、張り付いていることがわかると思います。
この結果から未知の問題に対しても先ほど紹介した式を使って期待値を更新していくことによって、理論上の期待値を推定できることが示されましたね。
では改めて以下の式をおさらいしてみましょう。
(学習率0.1として説明します。)
更新後の期待値=更新前の期待値×(1-学習率)+出た結果×学習率
もし、更新前の期待値が8、引いたカードの数が5だったとします。
更新後の期待値は8*(1-0.1)+5*0.1=7.7になりますね。
更新前の期待値8に対して、更新後の期待値7.7は理論上の期待値5.5に近づいていることがわかると思います。

だったら引いたカードが10だった場合は期待値から遠ざかるじゃないか。

その通りです。
しかしながら、更新前の期待値が8だった場合、そのように理論上の期待値から遠ざかるのは9か10が出たときだけですから、遠ざかることはありますが、その確率は低いのです。
なので、たまには理論上の期待値から遠ざかることはありますが、何度も試行回数を重ねれば最終的には理論上の期待値に近づいていきます。
いかがでしょうか?
何度も試行錯誤することによって、期待値を算出する方法&算出できるということをなんとなく理解していただけたのではないでしょうか。
試行回数と学習率の関係
先ほど紹介したプログラムには2つのパラメータがありました。
学習率(lr)と試行回数(trial_number)ですね。
今回紹介している方法で期待値を算出する際、これらをどう設定するかによって結果は大きく異なってきます。
そのあたりも実演しながらやってみようと思います。
まず学習率0.001で6000回試行した結果は以下の通りです。
(グラフの見方は先ほどと同じです。)

次に学習率を0.01に変更してやってみましょう。
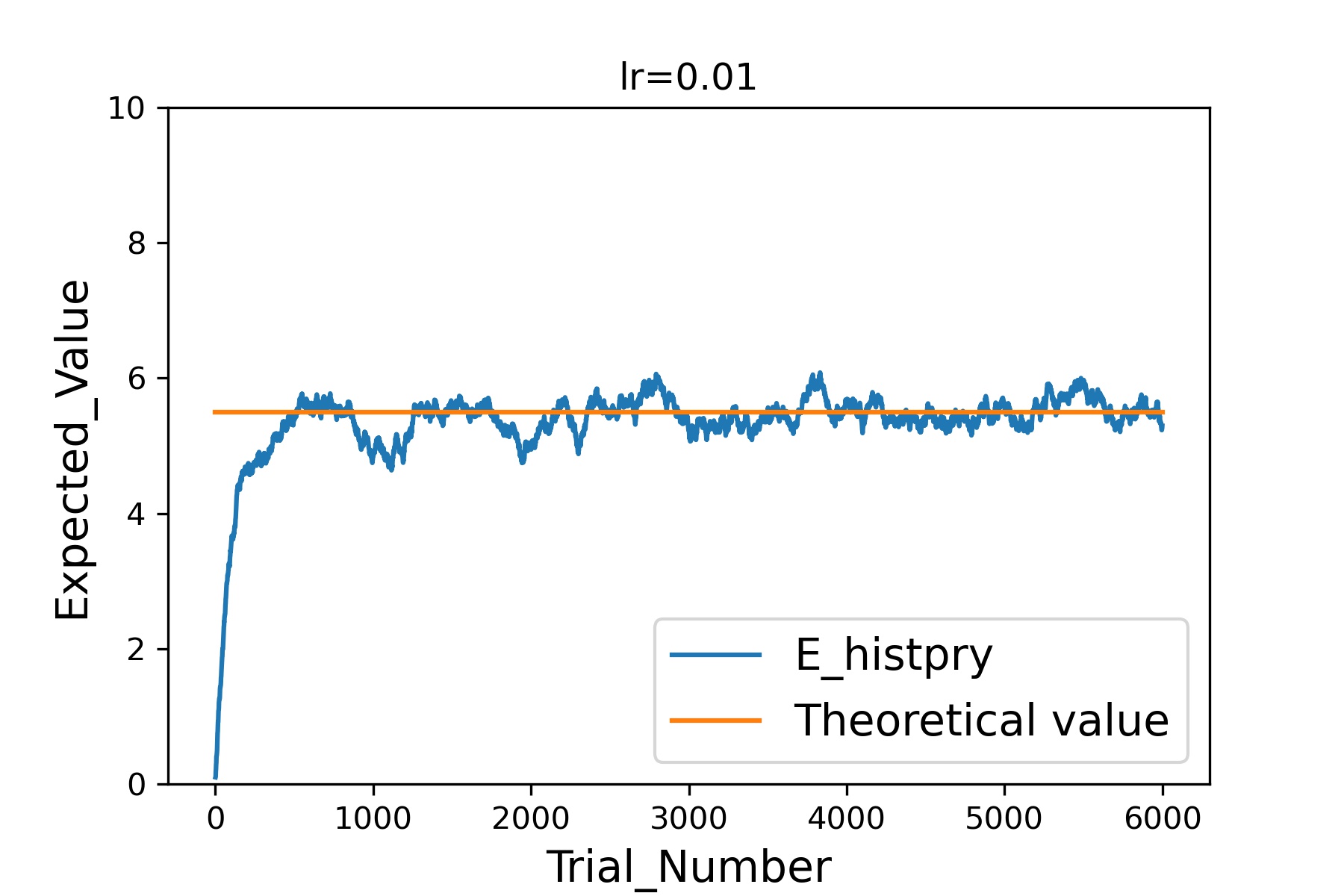
次は学習率0.1です。
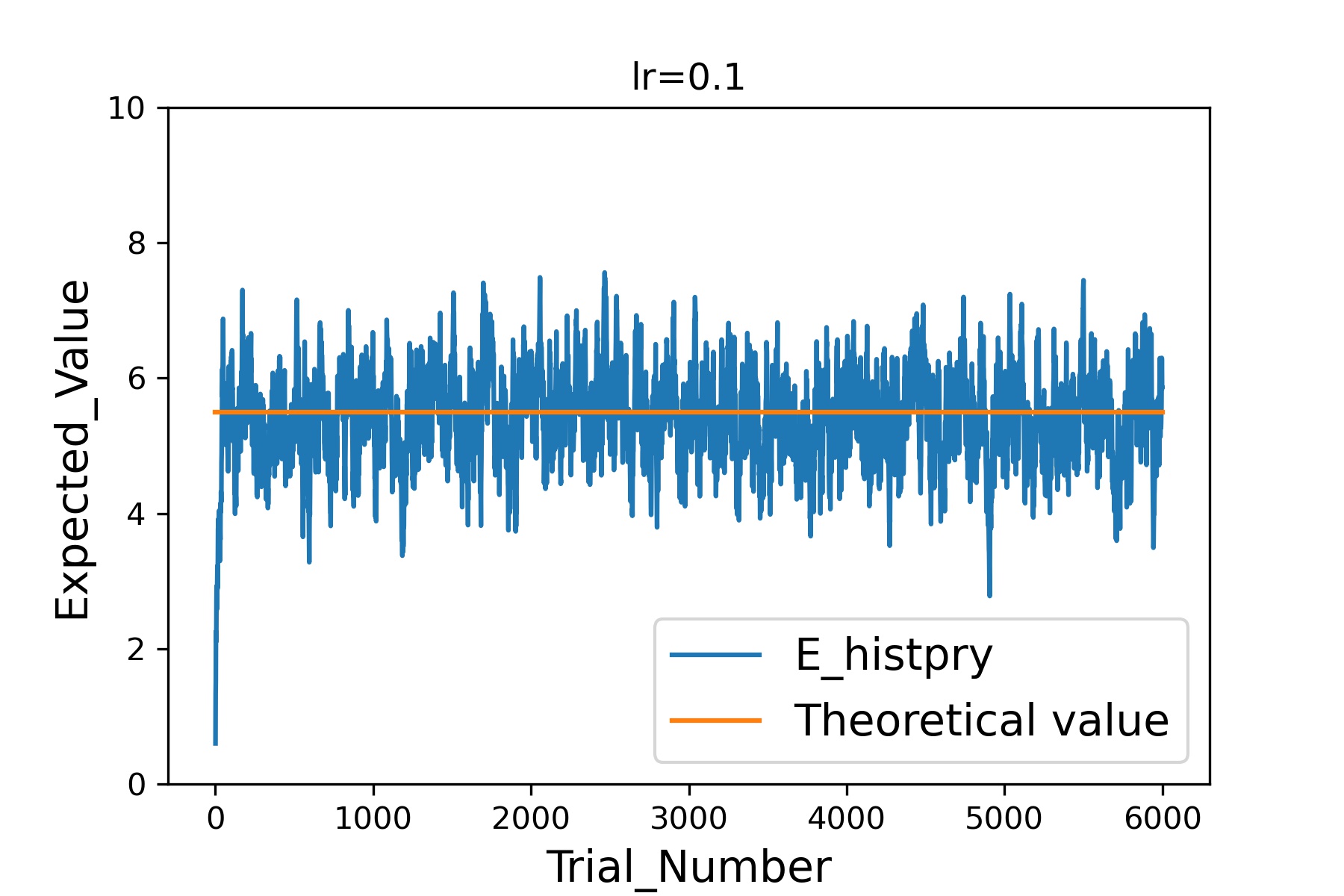
このように学習率を大きくしていくと、より少ない試行回数で理論上の期待値(オレンジ線)に近づくことができる一方で、近づいたあとのばらつきは非常に大きくなっていることがわかると思います。
このあたりは解きたい問題に応じて、速度重視なのか精度重視なのかを判断しながら設定する必要があるということですね。
おわりに
というわけで今回は強化学習の学習時に用いられる期待値の更新方法についてご紹介しました。
今後もAI関連の記事をご紹介していく予定ですので、ぜひブックマーク等していただけると幸いです。
それではまた!
★あわせて読みたい!
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村




コメント