
この記事では、座標を指定した3つの点からそれらの点によって形成されるなす角を計算する方法をご紹介します。
要は2つのベクトルのなす角を計算するということですね。
それではさっそくやっていきましょう。
計算内容の概要説明
冒頭の説明だけではどんな作業を行っていくのかイメージができていない人も多いと思いますので、絵を使って説明しておきます。
今回は以下の画像のように、3つの点の座標(x0,y0), (x1,y1), (x2,y2)を指定し、(x0,y0)と(x1,y1)で構成されるベクトルと(x0,y0), (x2,y2)で構成されるベクトルのなす角を求めていきます。
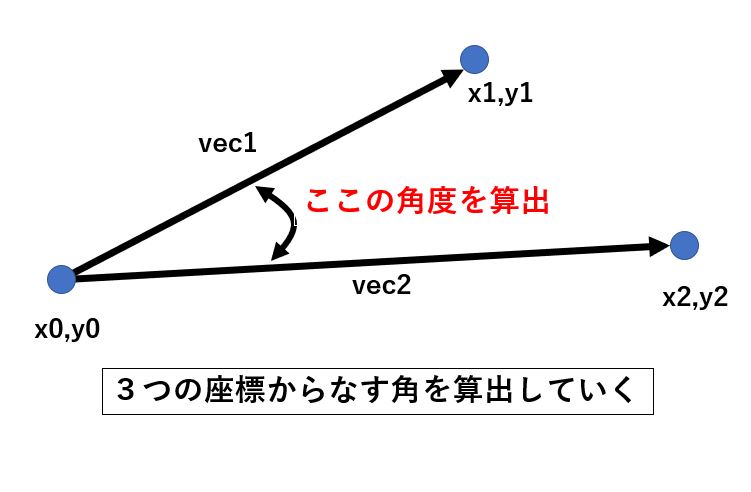
あなたのやりたいことと一致していれば、ぜひ続きをご覧ください。
2つのベクトルからなす角を計算する方法
pythonのコード紹介に入る前に、まずはどうやって角度を計算するのかを簡単にご紹介しておきます。
今回は高校数学でならった内積の公式を使って計算していきます。
以下が内積の公式です。
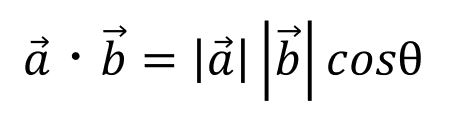
なんか見覚えありますよね。
要は内積はそれぞれのベクトルの大きさとなす角のcosをかけたものですよ~というものですね。
ここで内積(数式の左側)というのは、例えばベクトル(1,2)とベクトル(2,3)があった場合
1*2+2*3=8
という感じで計算できるものでしたね。
また、それぞれのベクトルの大きさは(数式の右側の絶対値で囲われている部分)は三平方の定理で計算できますよね。
つまり座標さえわかっていれば、内積の値とそれぞれのベクトルの大きさは計算できるということですね。
というわけで先ほどの数式を以下のように変換することによって、それぞれのベクトルがなす角θのcos値は計算できるというわけです。
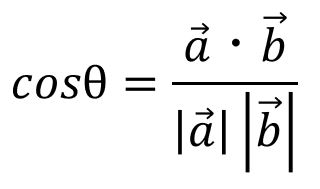
これさえわかればθを算出することは容易に可能ですよね。
(acosとか習いましたよね。)
というわけで今回はこういった数式を使ってなす角を計算していきます。
numpyでベクトル計算をする際の基礎知識
やり方はわかったと思いますが、先ほど紹介したようなベクトルの大きさや内積を一つ一つ計算するのは非常に面倒です。
しかしながら、ありがたいことにnumpyというライブライにはベクトルの大きさと内積を一発算出してくれる機能が備わっています。
まずはそれらの使い方をご紹介しておきます。
〇ベクトルの大きさを計算する方法
〇ベクトルの内積を計算する方法
これらをつかうことで面倒な計算を一発でやってくれます。
以降のプログラムでも出てきますので、覚えておきましょう。
3つの点の座標からなす角を計算するサンプルコード
前置きが非常に長くなりましたが、本題である3つの点の座標からなす角を計算するサンプルコードをご紹介します。
なお、このプログラム上の変数は以下の通りです。

要はx0,y0からそれぞれの点に向かって出ていくベクトルのなす角を計算するようになっています。
求めたい場所の座標をよく確認しながら入力するようにしましょう。
以下がそのサンプルコードです。
まずは2次元空間で計算した例です。
import math
import numpy as np
#2次元空間の場合
#角度の中心位置
x0,y0=0,0
#方向指定1
x1,y1=90,0
#方向指定2
x2,y2=0,90
#角度計算開始
vec1=[x1-x0,y1-y0]
vec2=[x2-x0,y2-y0]
absvec1=np.linalg.norm(vec1)
absvec2=np.linalg.norm(vec2)
inner=np.inner(vec1,vec2)
cos_theta=inner/(absvec1*absvec2)
theta=math.degrees(math.acos(cos_theta))
print('angle='+str(round(theta,2))+'deg')
こいつを実行すると
angle=90.0deg
が出力されました。
簡単な座標を入れているので問題なく計算できているのがわかると思います。
次は3次元空間で算出した場合です。
#3次元空間の場合
#角度の中心位置
x0,y0,z0=0,0,0
#方向指定1
x1,y1,z1=90,0,90
#方向指定2
x2,y2,z2=0,90,90
#角度計算開始
vec1=[x1-x0,y1-y0,z1-z0]
vec2=[x2-x0,y2-y0,z2-z0]
absvec1=np.linalg.norm(vec1)
absvec2=np.linalg.norm(vec2)
inner=np.inner(vec1,vec2)
cos_theta=inner/(absvec1*absvec2)
theta=math.degrees(math.acos(cos_theta))
print('angle='+str(round(theta,2))+'deg')
こいつを実行すると
angle=60.0deg
が出力されました。
ちょっと計算がむずかしいと思いますが、おそらく問題なく計算できているはずです。
さきほど紹介したinnerやlinalig.normが使用されていると思いますので、ぜひ作業内容を追いかけてみましょう。
おわりに
というわけで今回はpython上で、空間内で指定した3点がなす角度を算出する方法をご紹介しました。
実験データの分析の際などにぜひご活用ください。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント