
この記事では、pythonで2つの点の距離を一発算出する方法をご紹介していきます。
数学的に言うユークリッド距離ってやつですね。
2点間距離を計測する場合、いわゆる三平方の定理を使って計算しますよね。
その定理を再現するコードを書いてもOKですが、この記事で紹介する内容を使えば、そんなものは一行で記述できます。
実務でもときどき出くわす内容ですので、ぜひやり方を覚えておきましょう。
それではさっそくやっていいましょう。
numpyで2点間距離を計測する方法
いきなりですが、以下が二点間の距離を計測する方法です。
※a:1点目の変数、b:2点目の変数
変数a,bの次元は共通であれば何次元でもOKです。
以降、2次元、3次元配列にてこれを適用した際のサンプルコードをご紹介します。
2次元配列間の距離を計測するサンプルコード
それでは実際の使用例を紹介していきます。
まずは2次元配列に対して適用してみましょう。
今回は(x,y)が
a=(1,2)
b=(2,3)
という二点間の距離を計測してみます。
三平方の定理を使って計算すると答えは√2(1.41421356…)になるはずですね。
それではnp.linalg.normを使って検証してみましょう。
以下がそのサンプルコードです。
import numpy as np
a=np.array([1,2])
b=np.array([2,3])
distance=np.linalg.norm(b-a)
print(distance)※np.linalg.normの中はa-bにしても問題ありません。
こいつを実行すると以下の結果が出力されました。
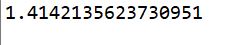
問題なく√2である1.41421356…が出力されてますね。
3次元配列間の距離を計測するサンプルコード
次は先ほどのコードを3次元配列に変更してみましょう。
今回は(x,y,z)が
a=(1,2,3)
b=(2,3,4)
という二点間の距離を計測してみます。
これも三平方の定理を使って計算すると、答えは√3(1.7320508…)になるはずですね。
np.linalg.normを使って検証してみましょう。
以下がそのサンプルコードです。
import numpy as np
a=np.array([1,2,3])
b=np.array([2,3,4])
distance=np.linalg.norm(b-a)
print(distance)※np.linalg.normの中はa-bにしても問題ありません。
こいつを実行すると以下の結果が出力されました。
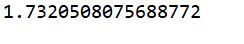
問題なく√3である1.7320508…が出力されてますね。
おわりに
というわけで今回はpythonで2点間距離を計測する方法をご紹介しました。
今回は3次元までしか紹介していませんが、基本的には4次元、5次元と拡張していくことも可能です。
ぜひコードを書き換えて実行してみましょう。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント