
この記事では、エクセルとpythonを使ってFFT解析について解説していきます。
◇この記事の内容
〇そもそもFFT解析とは?
〇FFT解析って何につかうの?
〇FFTで出てくる波の周波数とは?
〇pythonでのFFT解析の実行方法
画像を使って詳細解説していきますのでぜひ最後までご覧ください。
※「FFT解析くらい知ってるわ。やり方だけ教えてくれ!」という方は最後の方まで飛ばしちゃってください。
それではさっそくやっていきましょう。
そもそもFFT解析とは?
まずはFFT解析とは何なのかをご紹介します。
まず前提として周期的な波はどんな形であれ、単純なSIN波の足し算で表現できます。
例えば以下の波は2SIN(θ)+SIN(2θ)で計算されたもの。
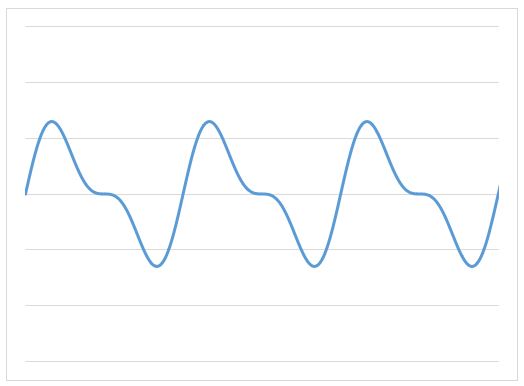
また、以下の波は2SIN(2θ)+SIN(θ)+3SIN(3θ)で計算されたものです。
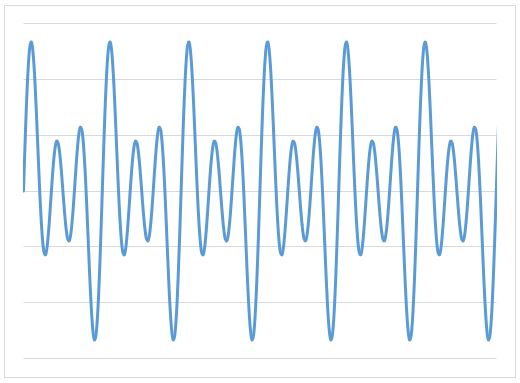
こんな感じでどんな波であっても合成する波を増やしていけば表現することが可能です。
今回紹介するFFT解析とは、先ほど紹介した例を逆方向に実施するものだと思えばOKです。
具体的に説明します。
例えば、何かしらの実験をして以下の波形が得られたとします。
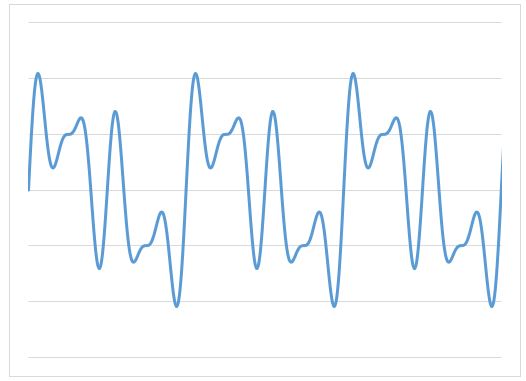
この波形をFFT解析すれば、
この波は、
2SIN(4θ)+SIN(2θ)+SIN(6θ)+2SIN(θ)
で表されますね、ということがわかります。
ものすごくざっくりとFFT解析とは何か?を説明するとこんな感じです。
要は、複雑な波を構成するSIN波を取り出していく作業ですね。
FFT解析って何につかうの?
次に、FFT解析はどのように使われているのかを解説していきます。
説明をわかりやすくするために、まずは身近な音の波について解析します。
ご存じの方も多いと思いますが、音というのは空気が波のように振動することによって耳に届いています。
そしてその波は周波数(波の山と山の間隔)に応じて高い音、低い音というのが決まっています。
また、その波の振幅(山の大きさ)によってどのくらい大きな音かが決まります。
次にFFT解析の説明に戻ります。
先ほど紹介したFFT解析で得られるSIN波はすべて以下の形で得られていたと思います。
A×SIN(Bθ)
ここでのAがいわゆる振幅です。
また、Bが周波数です。(厳密な定義は少し違います。後程、詳細説明します。)
つまりFFT解析をすれば、合成された波がどのような周波数と振幅を持っているかを分析することができる、というわけですね。
ここまでの話をまとめると、例えば耳に届いている音の波をFFT解析することによって、発生している音の周波数(音の高さ)と振幅(音の大きさ)がどうなっているかがわかります。
そしてそれらがわかることによって、耳に届いている音の発生源を特定できたり、音の低減につながっていくわけです。
工学の分野ではこんな感じでFFT解析が活躍しているわけですね。
波の周波数とは?
先ほどFFT解析によって得れれるA×SIN(Bθ)において、Aが振幅、Bが周波数であると説明しました。
しかしながらBとかθとかの概念をもったままFFT解析に入ってしまうと混乱を招いてしまいますので、FFT解析におけるBとかθの取り扱いについて解析しておこうと思います。
では早速解説に入ります。
そもそもθというのは高校数学で出てきたいわゆる角度を表すものですよね。
一般的に良く見る以下のSIN波も横軸はθだと思います。
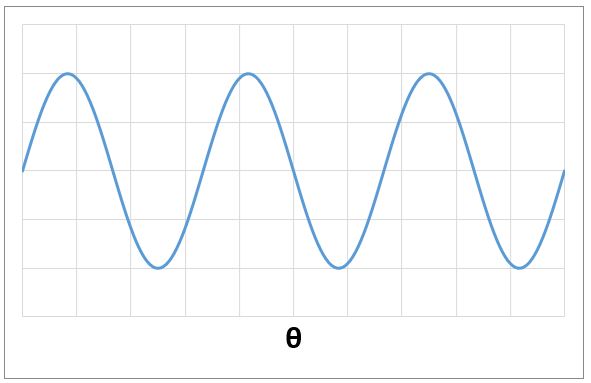
ですが、実世界で観測されるこのような波というのは横軸が時間で現れてきます。
つまりこの角度θを時間tに変換しなければいけないわけですね。
ここで出てくるのが角速度(ω)という概念です。
角速度は回転する物体が1秒間に何回転するかという指標ですね。
つまりω=1であれば1秒間に一回転、つまり360deg回るということですね。
この考えを使えば、角度軸を時間軸に変更できそうだということがわかると思います。
理解を深めるためにこのあたりからはもうエクセルで実演してしまいましょう。
以下の絵はω=1においてSIN(2πωt)をグラフ化したものです。
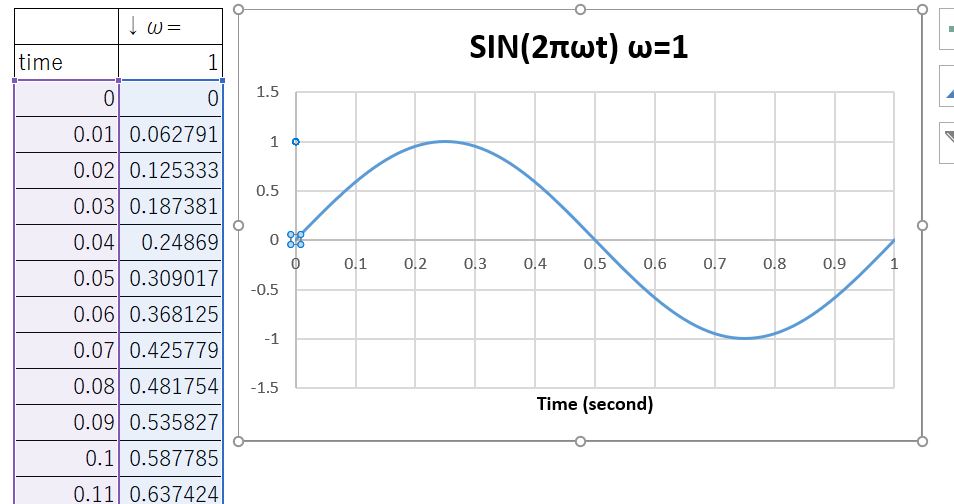
数式欄にはこんな感じで記述されています。
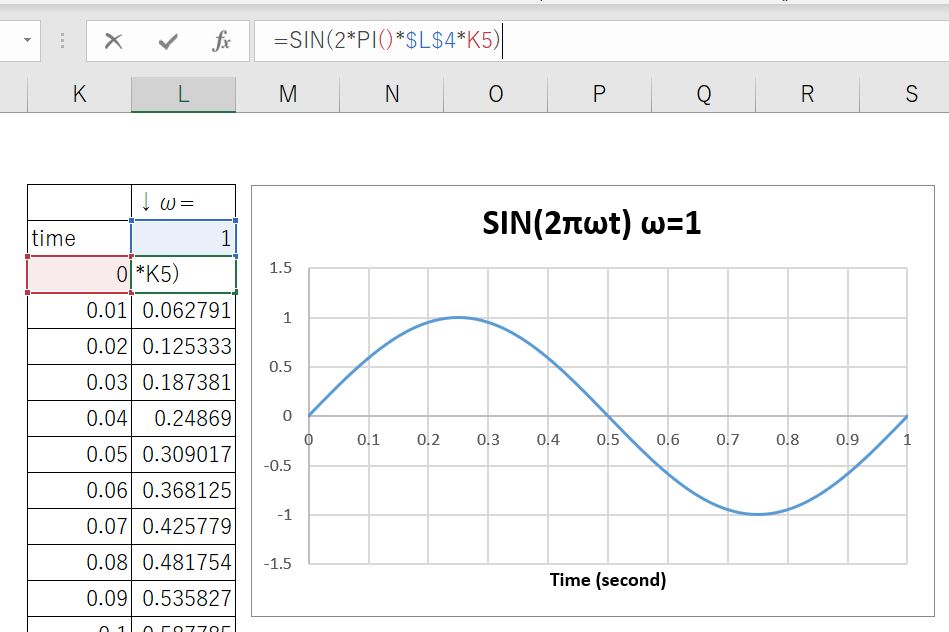
こんな感じで1秒間で山が1回、谷が1回の波を形成できていることがわかります。
周波数とは、1秒間に何回波が到達したか、を示すものですので、この場合、周波数=1の波が計算されているというわけです。
つぎにこのエクセルシートのωを2に変更してみましょう。
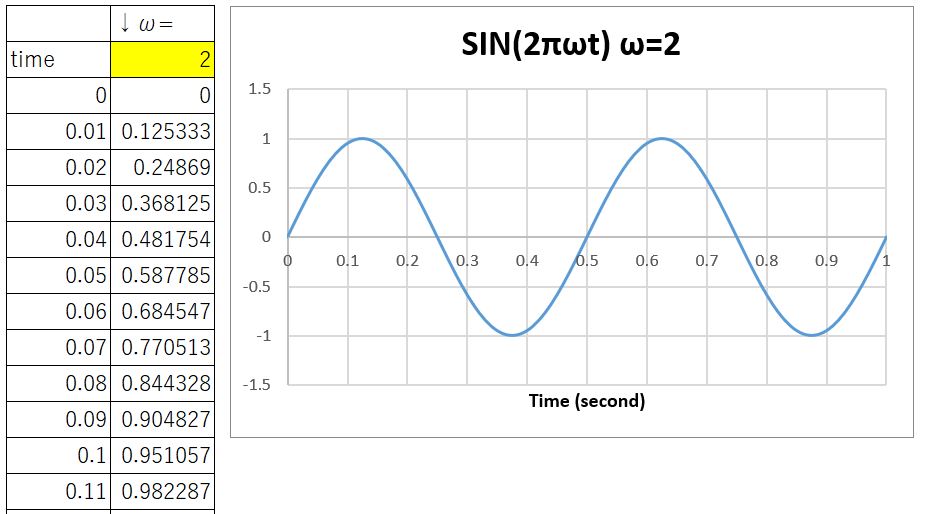
すると1秒間に山が2回、谷が2回になったことがわかります。
つまり周波数=2になったというわけですね。
ωを3にしてみましょう。
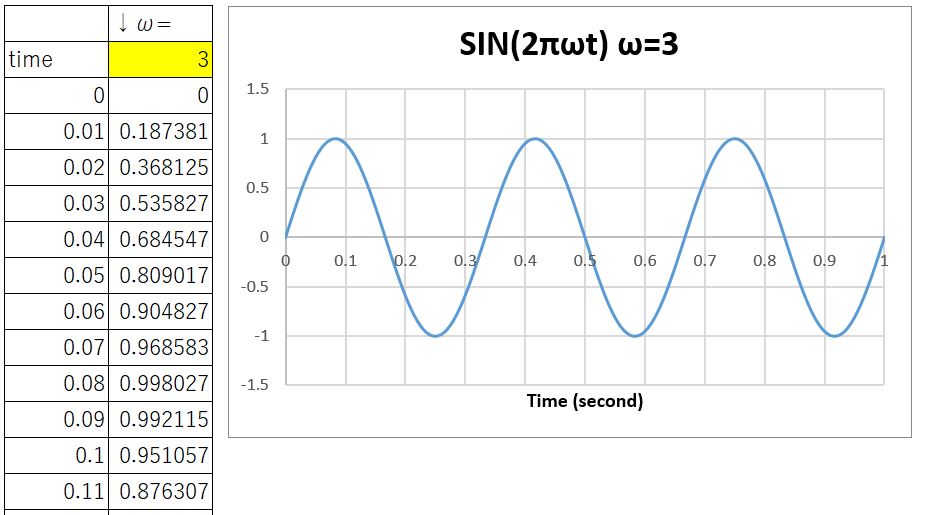
1秒間に山が3回、谷が3回になったことがわかります。
つまり横軸を時間軸にとった場合、SIN(2πωt)のωが周波数になってくれるわけです。
以降で紹介するpythonでのFFT解析ではこのωが出てきます。
前置きが長くなりましたが、最後に実際にpythonを使ってFFT解析を実行してみましょう。
pythonでのFFT解析の実行方法
実行する前に、まずはデータを準備しましょう。
まずは先ほど紹介したようにA×SIN(2πωt)の波をAとωを変えながらいくつか作成します。今回は以下のような流れで適当な合成波を作成しました。
STEP1_適当なSIN波を作成
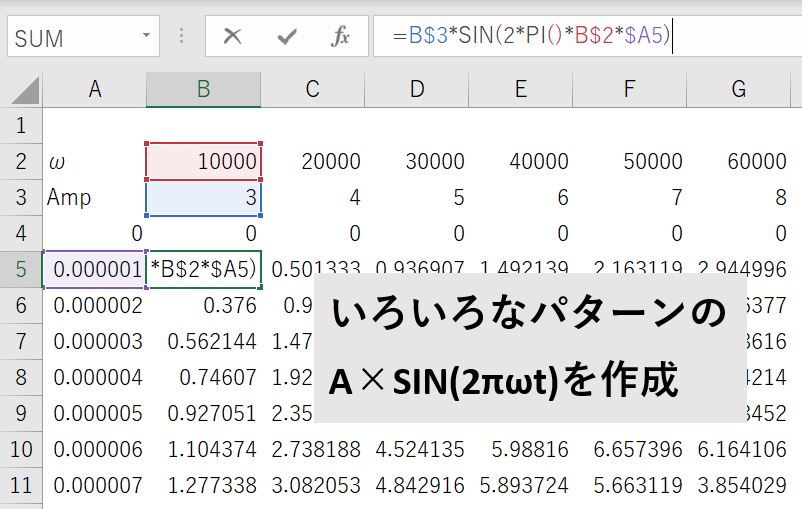
STEP2_作成したSIN波を合成する
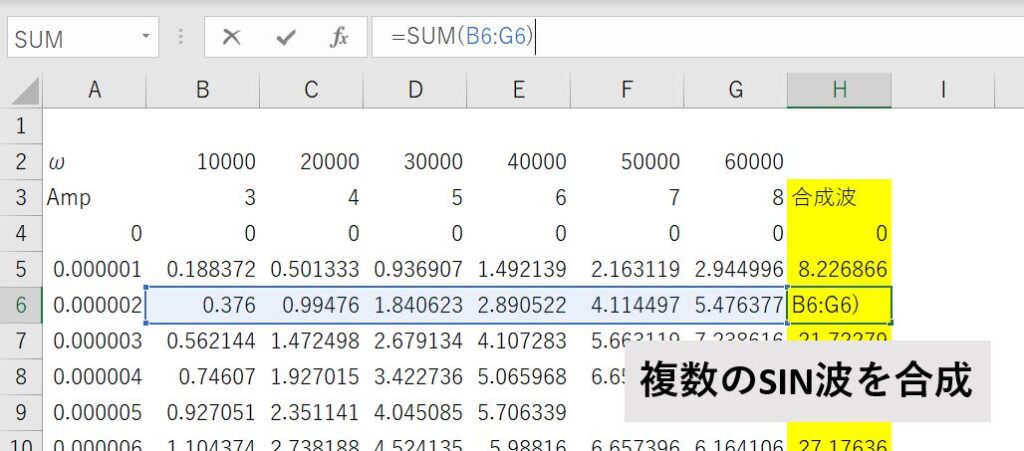
合成された波は以下のような時系列データになります。
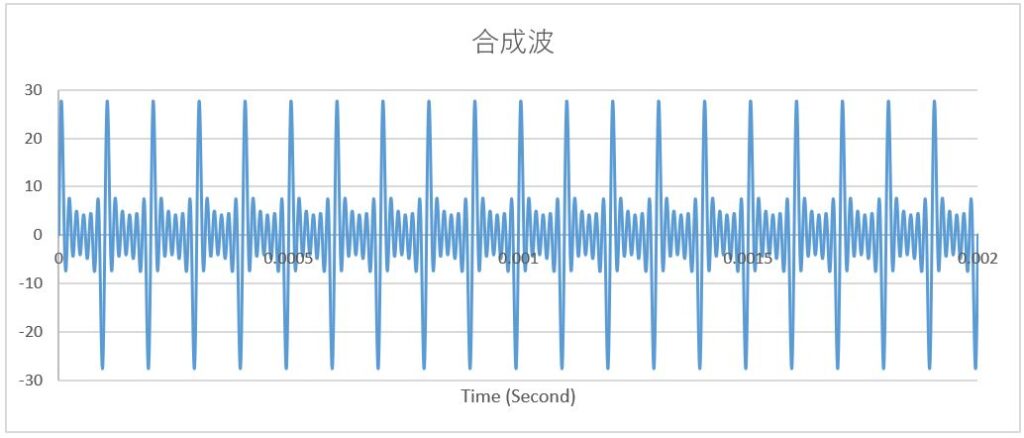
この時系列データをいったんテキストファイルにでも保存しておきましょう。
時間軸についてはpython上で指定しますので、波の振幅だけでOKです。
(今回はdata.txtという形で保存しています。)
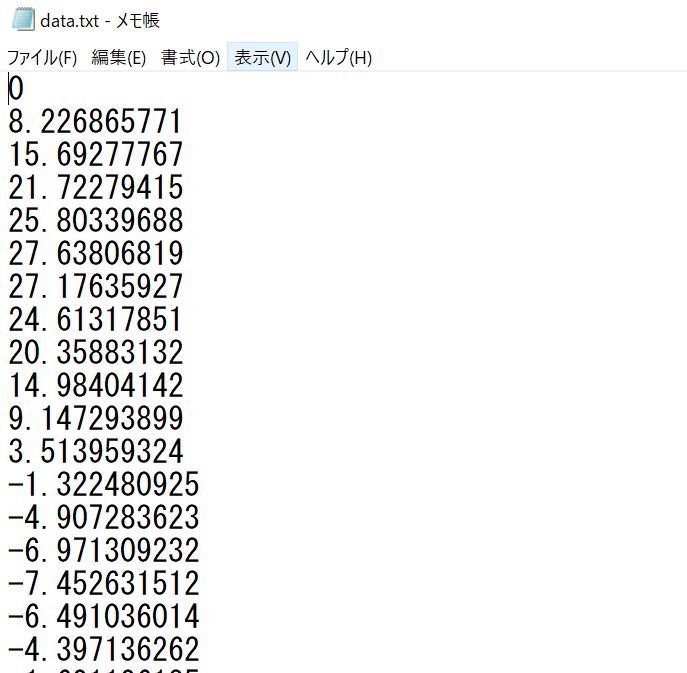
事前準備はここまで。
それでは実際のコーディングに入っていきましょう。
今回は以下のようにpythonの実行コードと先ほど作成したFFT解析するデータが同じフォルダにあることを想定してコードをかいています。
data.txtが適当な合成SIN波のデータが入っているファイル、FFT_test.pyがこれから紹介するコードが記述されているファイルです。
以下がFFT_test.pyの中身になります。
# ライブラリインポート
import numpy as np
import matplotlib.pyplot as plt
# データ読み込み_dt指定
data=np.loadtxt('data.txt')
num_data = len(data)
dt = 0.000001
Hz = np.linspace(0, 1.0/dt, num_data) # 周波数軸
# FFT解析
FFT = np.fft.fft(data)
Amp = np.abs(FFT)
Amp = Amp / num_data * 2
# グラフ作成
plt.figure()
plt.rcParams['figure.subplot.bottom'] = 0.2
plt.plot(Hz, Amp)
plt.xlabel('Hz', fontsize=14)
plt.ylabel('Amp', fontsize=14)
plt.xlim(0,80000)
plt.grid()
plt.savefig('graph.jpg',dpi=200)
このコードを実行すると、実行フォルダには以下のようなグラフが出力されていました。

なにらやそれらしい感じにはなっていますね。
もとのエクセルファイルと比較してみましょう。
以下がFFT解析に使った波形を作ったときのデータです。(ωとAmpをご確認ください。)
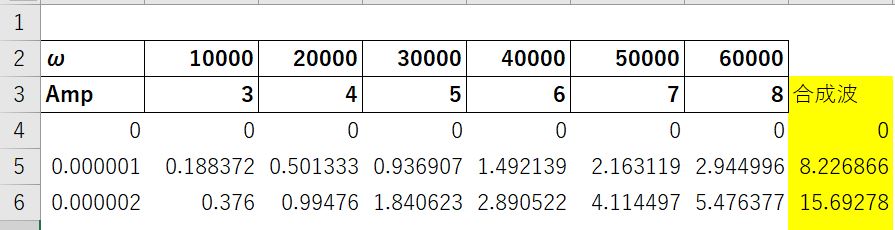
両者を比較してみると、山が立つ場所がω、山の大きさがAmpに対応していることがわかると思います。
つまり、この結果から問題なく合成波の周波数と振幅を算出できていることが確認できたわけです。
おわりに
というわけで今回はpythonを使って、適当な合成波をFFT解析してみました。
音響解析の際などにぜひご活用ください。
このように、私のブログでは様々なスキルを紹介しています。
今は仕事中で時間がないかもしれませんが、ぜひ通勤時間中などに他の記事も読んでいただけると嬉しいです。
⇒興味をもった方は【ヒガサラ】で検索してみてください。
確実にスキルアップできるはずです。
最後に、この記事が役に立ったという方は、ぜひ応援よろしくお願いします。
↓ 応援ボタン
![]()
にほんブログ村
それではまた!
Follow @HigashiSalary




コメント